PS-13 String

1. 串

实际上就是字符串

2. 模式匹配

$Text$和 $Pattern$的匹配

蛮力算法

抓住 $Pattern$的头，和 $Text$串的每个元素逐一比对，如果匹配成功再深入 $Pattern$串比对

最好情况： $\Omega (n)$

最坏情况： $O(n\cdot m)$

KMP算法

关键在于构建一个表，记录每个位置如果匹配失败，则更新成 $Pattern$串的 $j$前面的哪一个元素，即 $t$

查询表

当前 $j$个元素已经匹配时，我们只需找到在已匹配的串中，最长的前缀和后缀自匹配，然后就能确定 $t$，依此来构建查询表 $next[0,m)$，在 $j$处失配，将其换为 $next[j]$即可

$next[0]$恒为-1

为什么要取最长的自匹配？为了使移动的距离最小，不至于回溯

构造next[]表

next[0]必然恒为-1，属于通配符

next[1]按照规则也必然为0

当已知next[0]，…，next[j]时，如何确定next[j+1]？

其实就是让0~j去自匹配，先看j和next[j]是否匹配，如果匹配next[j+1]就在next[j]的基础上+1，如果不匹配，就再看j和next[next[j]]是否匹配，匹配则在此基础上+1，否则继续查询下去

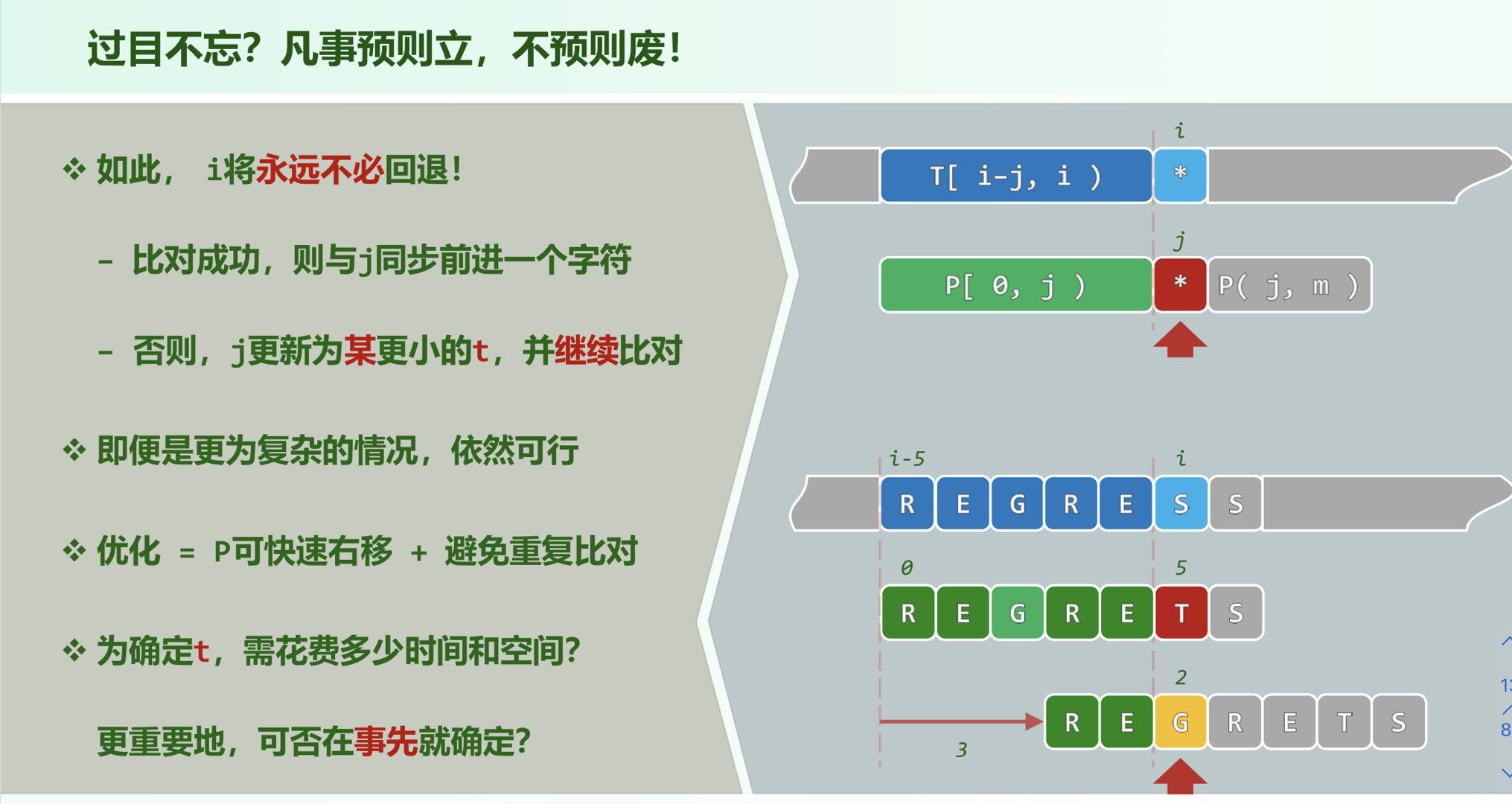
复杂度

绿色和红色的比对，落到一条线上也不过 $O(n)$，需要考虑的是黄色的比对

怎么设计出来的？？？

再改进

KMP算法有一种很笨的情况，就是j和next[j]的元素是一样的，这样会导致在替换过后也必然失配，我们要避免这样的情况发生

在构造查询表时，在每个元素赋值之前，要先看这个元素和赋值的元素是否相等，否则要赋将赋值元素的next[]（由于不变性，赋值元素的next[]必然与其本身不相等，因此这样一次即可）

注意

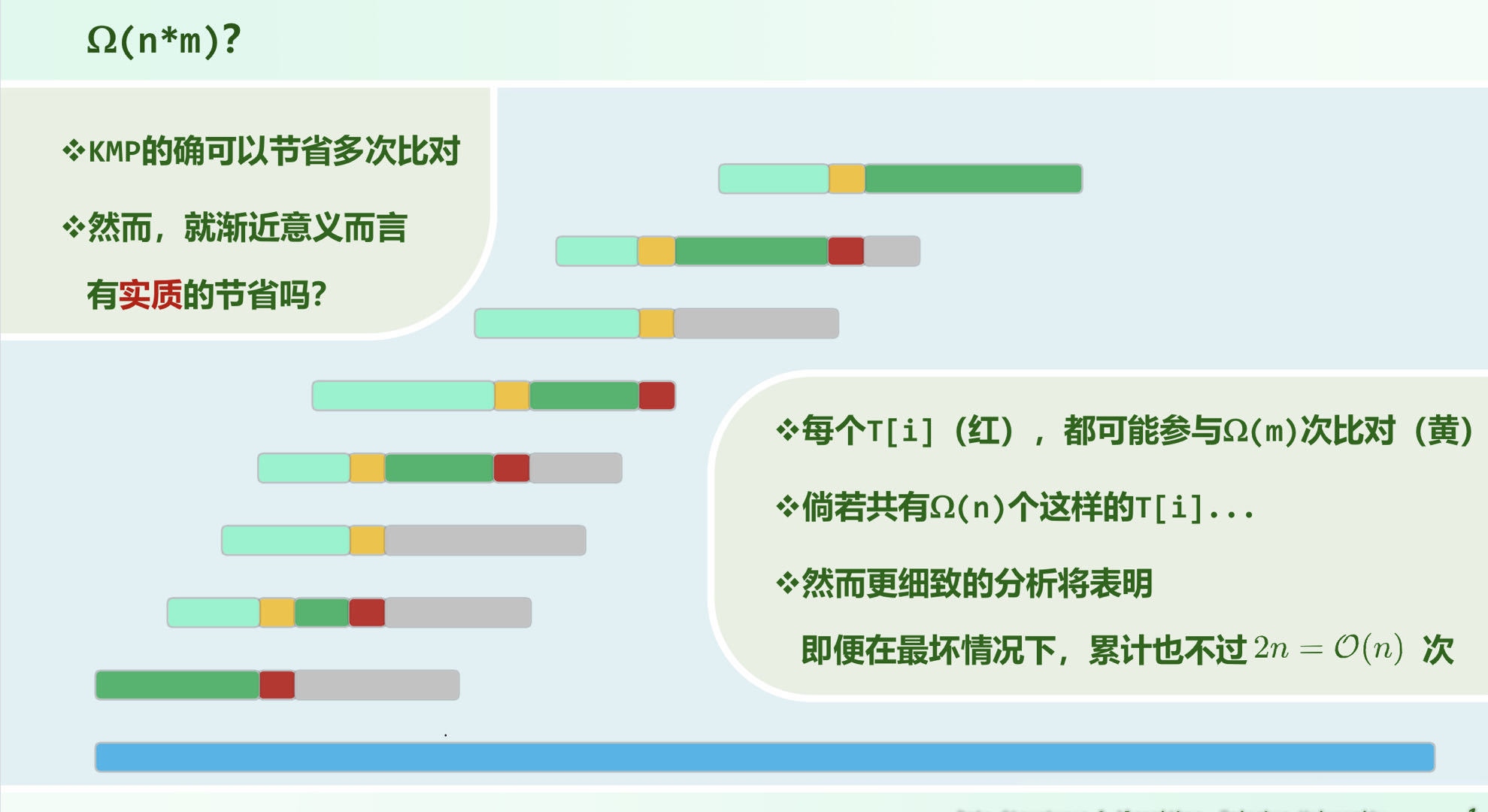
当匹配的字符集越小，成功的概率越大，KMP算法的优势才明显，否则蛮力算法期望上来讲也不过走两步，性能也是 $O(2n)$

BM算法：BC策略

每次比对从 $Pattern$的末尾开始，如果发生失配，找到 $Pattern$失配位置前有没有对应失配位置 $Text$的字符，如果有则移动到对应位置，再从后往前比对，没有则整体后移

bc[]表

构造字符集的哈希表，对应字符存入 $Pattern$中秩最大的位置，在应用时，如果 $Text$字符在 $Pattern$失配位置之后，则 $Pattern$只移动一位即可

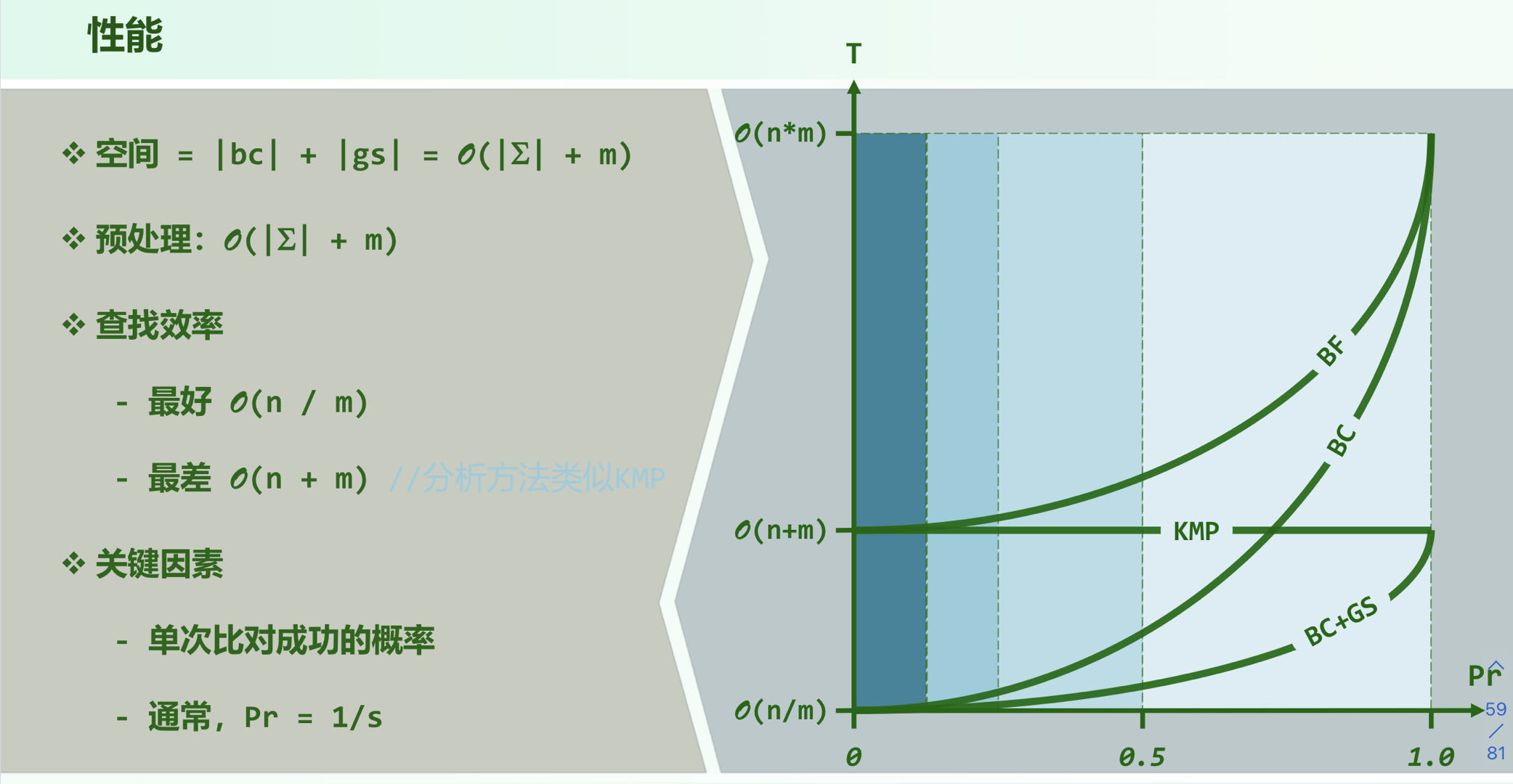
性能

$O(n/m)$

最差仍是蛮力算法

单次匹配概率越小，P越长，优势越明显

BM算法：GS策略

找到匹配后缀的自匹配（或部分匹配）前缀，与KMP的策略相同

性能比较

3. Karp-Rabin算法

串即是数

哥德尔的思想，世间万物都能用自然数来表示！

散列

将 $Text$串的每一指纹换算成数，再用 $hash()$压缩存入散列中，把 $Pattern$也转化，再与散列比对，比对成功之后，再取出原指纹比对

相邻指纹之间的散列可由上一指纹求出下一指纹，比如求余，减去头的影响，加上尾部的影响即可

4. 键树

？？？