PS-12 Priority Queue

1. 优先级队列

基本实现

使getMax()，delMax()，insert()均只需 $O(logn)$的时间，并且实现起来很简单，不必维护全序关系

完全二叉堆

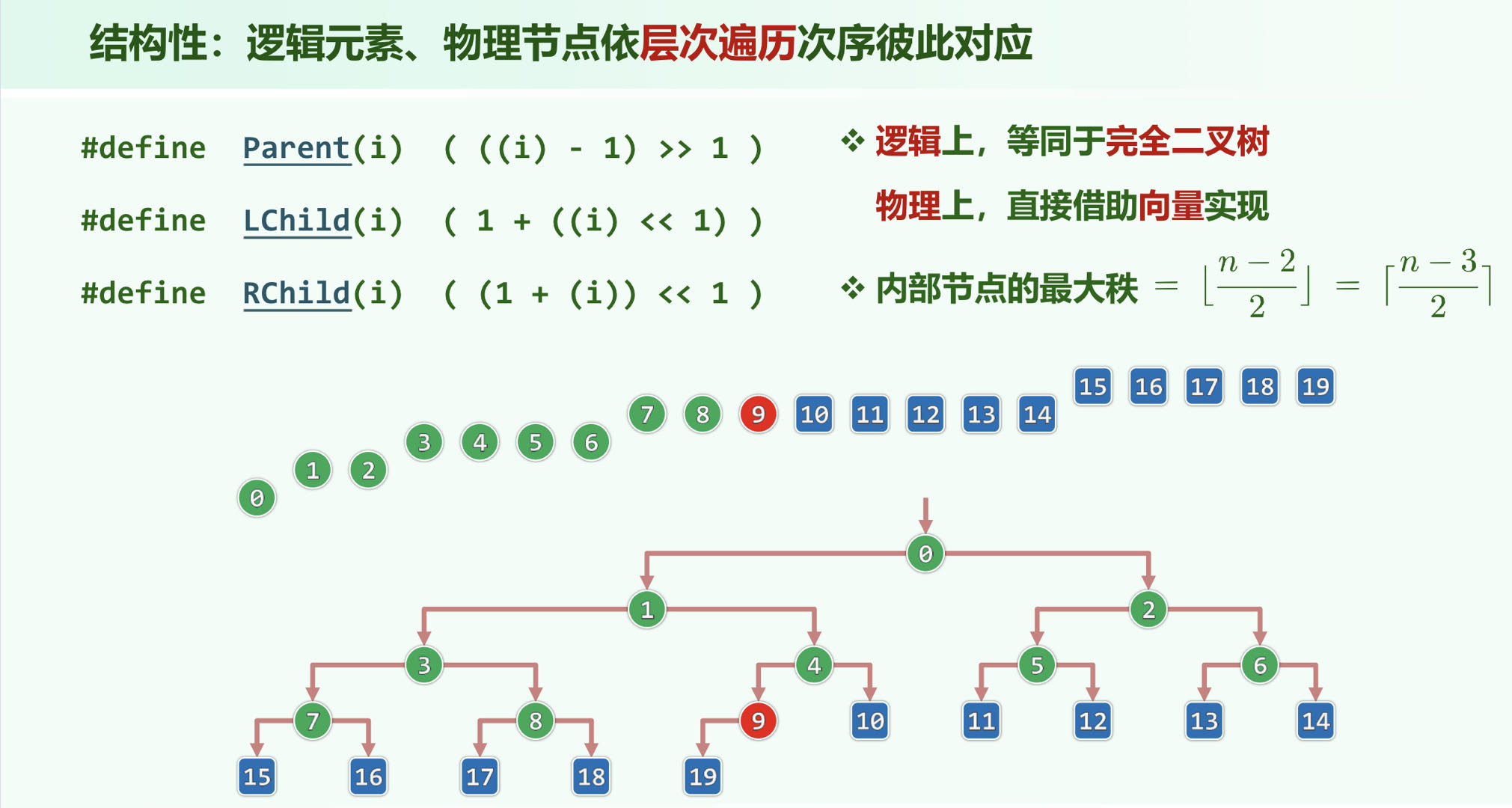
要求在逻辑意义上， $\forall i,H[i]≤H[parent(i)]$

插入

先在尾部插入，然后和其逻辑次序的父亲比较，如果更大则交换，然后就这样一层一层比较，逐层上滤，直到不大于父亲或到达顶端，所需时间为 $O(logn)$

删除

接口只实现删除极大元素即顶部元素，将尾部元素拿到顶上来，然后与其逻辑的两个孩子比较，取三者中的最大者当父亲，就这样逐层下滤，直到满足条件为止，所需时间为 $O(logn)$

2. 批量建堆

自上而下的上滤（蛮力算法）

自顶层元素，逐一上滤，最终建堆

但是所需时间会达到 $O(nlogn)$，那还不如直接全排序

自下而上的下滤

从尾部的内部节点开始，从后往前逐一下滤，最终建堆

不变性：顶层元素下滤到两个满足堆序性的子堆中，全局必然满足堆序性

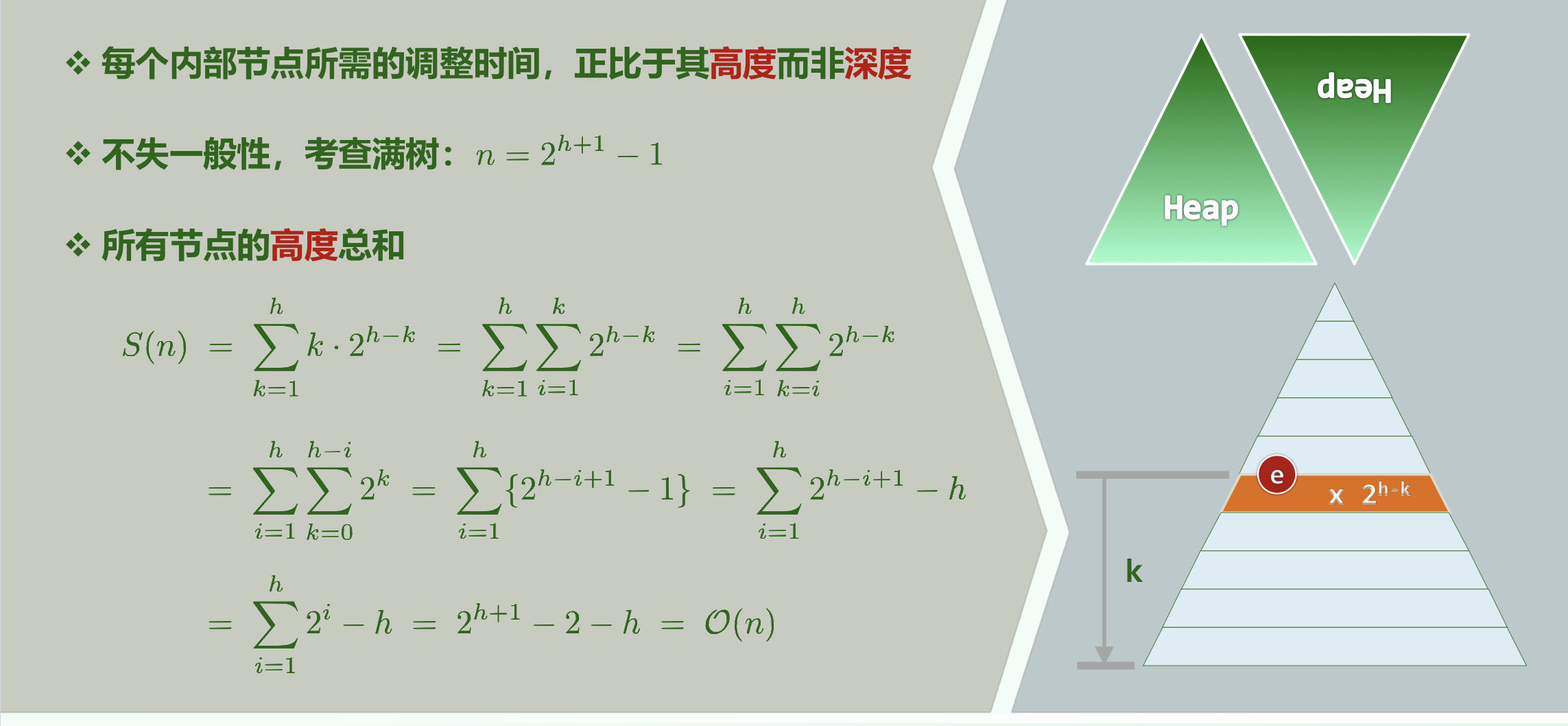
在这种情况下，每个内部节点下滤所花时间正比于其高度而非深度，而高度低的内部节点更多，所以显然比正比于深度的蛮力算法更省时间

思考

insert()最坏情况是 $O(logn)$，平均情况是多少？

平均情况下，由于有一半的元素分布在最底层，插入一个元素向上攀升一层的概率是 $1/2$，这样攀升高度构成了一个几何分布，平均高度为 $O(2)$

3. 堆排序

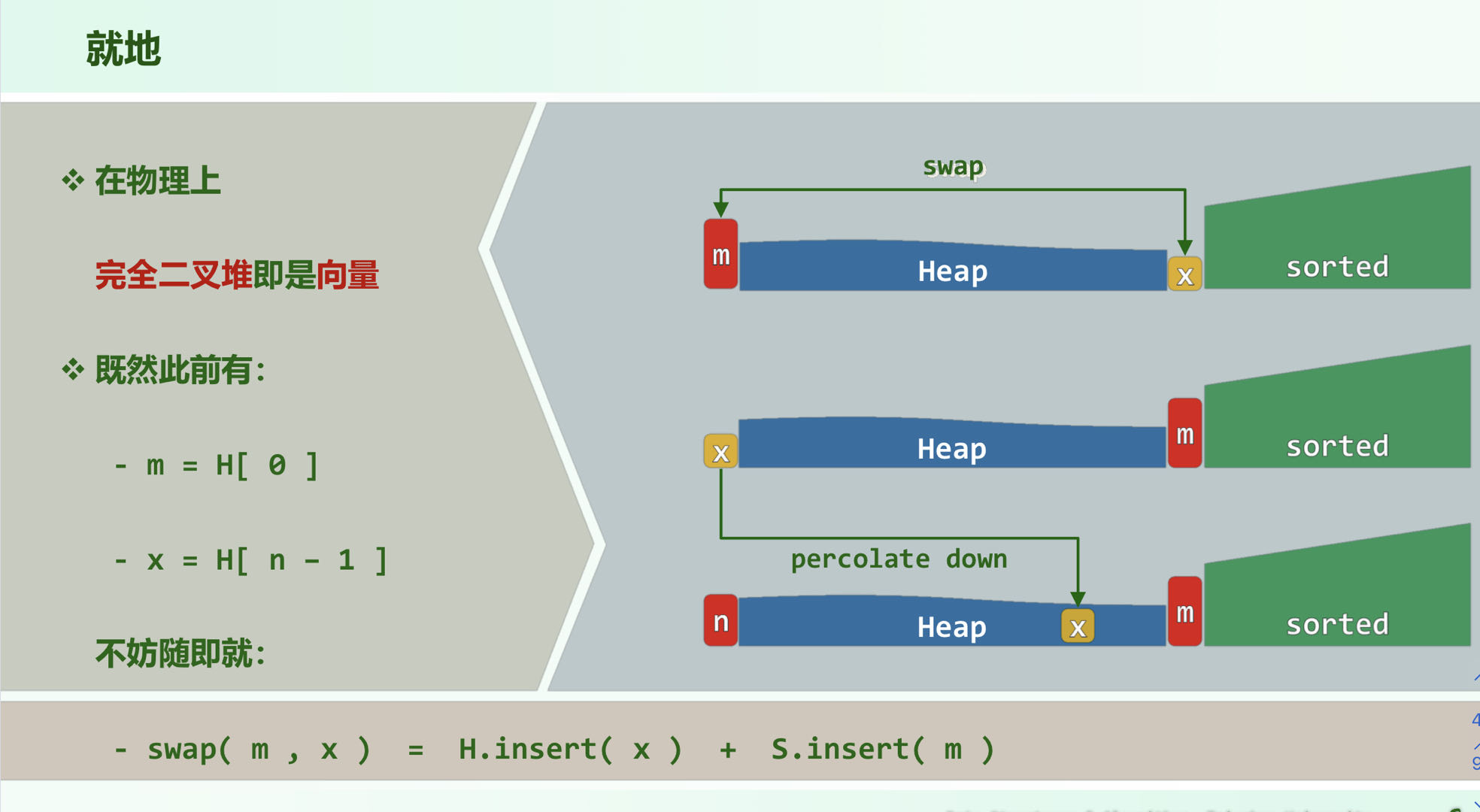
首先整体序列构造成一个完全二叉堆，然后逐一删除顶部元素（实际上就是把极大元素扔到尾部去），这样就实现了整体的堆排序

复杂度是 $O(n+nlogn)$