PS-08 Advanced Search Trees

1. Splay Tree（伸展树）

由于访问的局部性，访问一个节点以后可能不久就再次访问，于是把每次访问的节点移到树根，这样的树叫做伸展树

每次移动都要通过zig,zag一层一层地爬上去，如果周期性地访问，分摊复杂度可达 $\Omega (n^{2})$

双层伸展

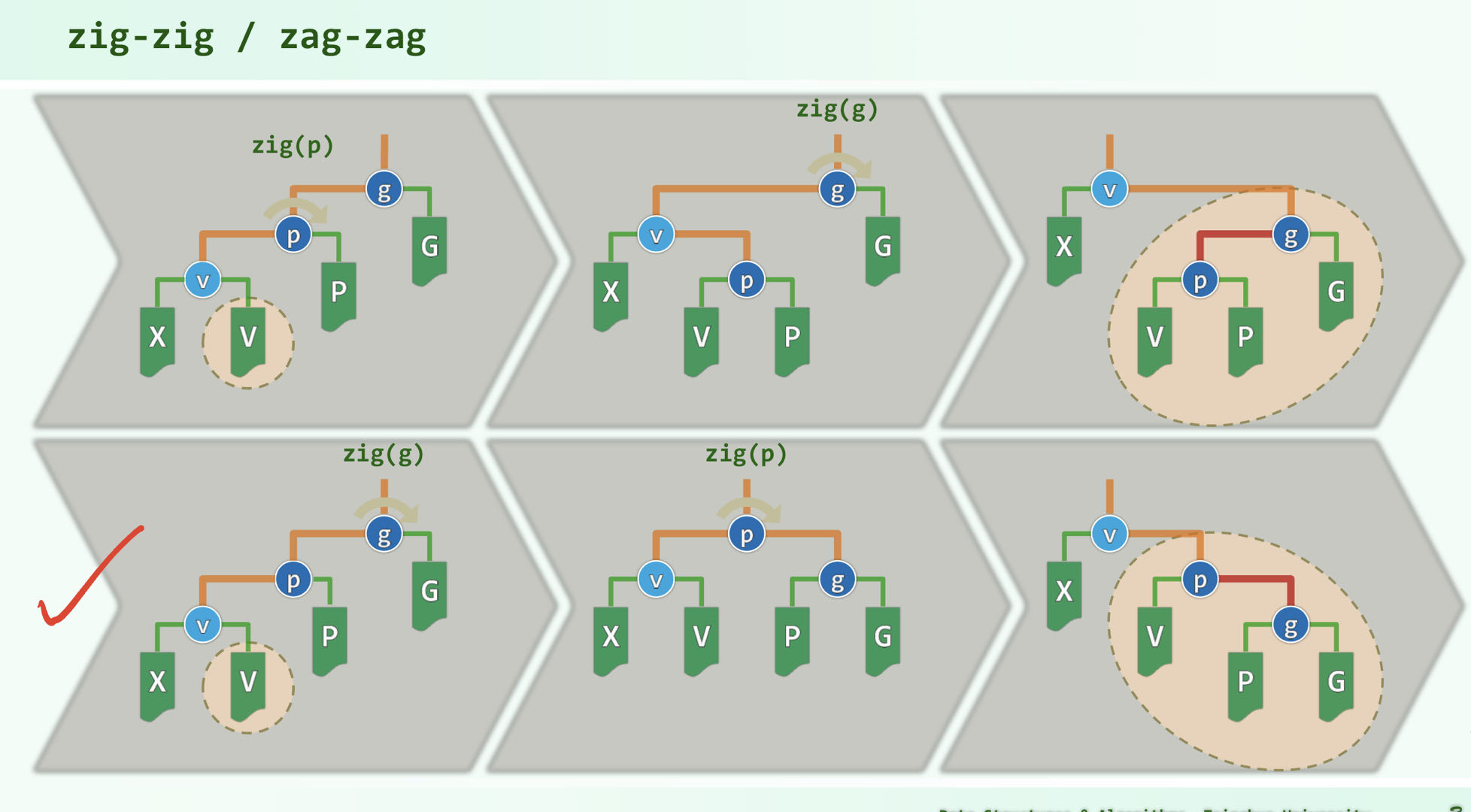
每次伸展要一起看两层，从祖父旋转

插入

先通过search()找到不大于插入节点的最大节点并伸展至根，然后再在根的头上生成新节点

删除

通过search()找到目标节点，伸展至根然后删除，删除后从右子树中找到最小节点伸展至根作为新的根

复杂度

分摊复杂度为 $O(logn)$

分析

运用势能分析法

2. B树

• 存储器规模增长速度远远小于问题规模增长速度
• 增大存储器规模会使访问速度变慢
• 存储器有内部级联结构，不同级联结构访问速度不同，访问内存1s，访问磁盘则需要一天
• 相邻存储级别之间的数据传输在算法时间中占的更多

结构

每d代合并为1个超级节点，每个节点有 $m=2^{d}$条支路， $m-1$个关键码

内部节点分支个数为 $m/2≤n≤m$，关键码个数为 $n-1$

但是根节点关键码个数 $n≥1$即可

查找

在每个节点中顺序查找，查找失败则转到下一层继续查找（相当于1次I/O操作）

运行时间 $O(logn)$

插入

先通过search()找到插入位置，如果上溢，取出中位数关键码移到上层，原节点分裂为两个

若父亲也上溢，用同样的办法分裂，若上溢向上传播，则逐层解决直到根

删除

先通过search()找到删除位置，如果不是叶子节点，则找到直接后继与其交换，然后在直接后继的位置将其删除

如果下溢，看左右兄弟的规模：

• 如果左兄弟有盈余，将左兄弟的最大关键码移到父亲节点上来，将父亲节点的分界关键码移到被删除的节点中
• 如果右兄弟有盈余，将右兄弟的最小关键码移到父亲节点上来，将父亲节点的分界关键码移到被删除的节点中
• 如果左右兄弟都不够，则选择左兄弟或右兄弟，将其父亲的分界关键码拿下来两个节点合并为一个节点，但可能引起向上传播，则逐层修复

3. 红黑树

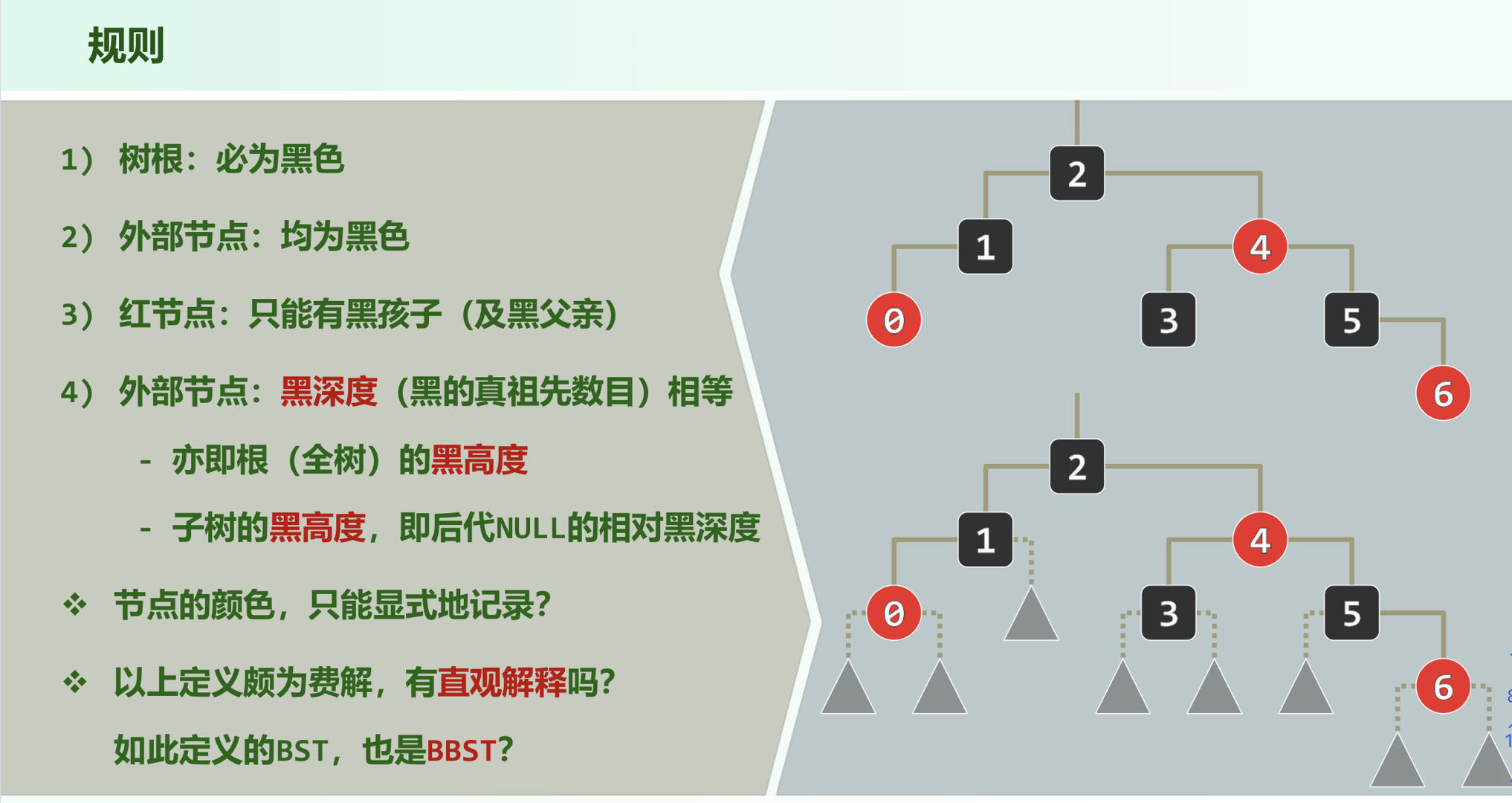
将红节点高度提升至与其黑父亲等高，实际上相当于一个(2,4)-B树，也是BBST

插入

search()找到插入位置，然后染红（根节点要染成黑的），此时规则3可能会违反，可能会出现双红的情况

双红修正

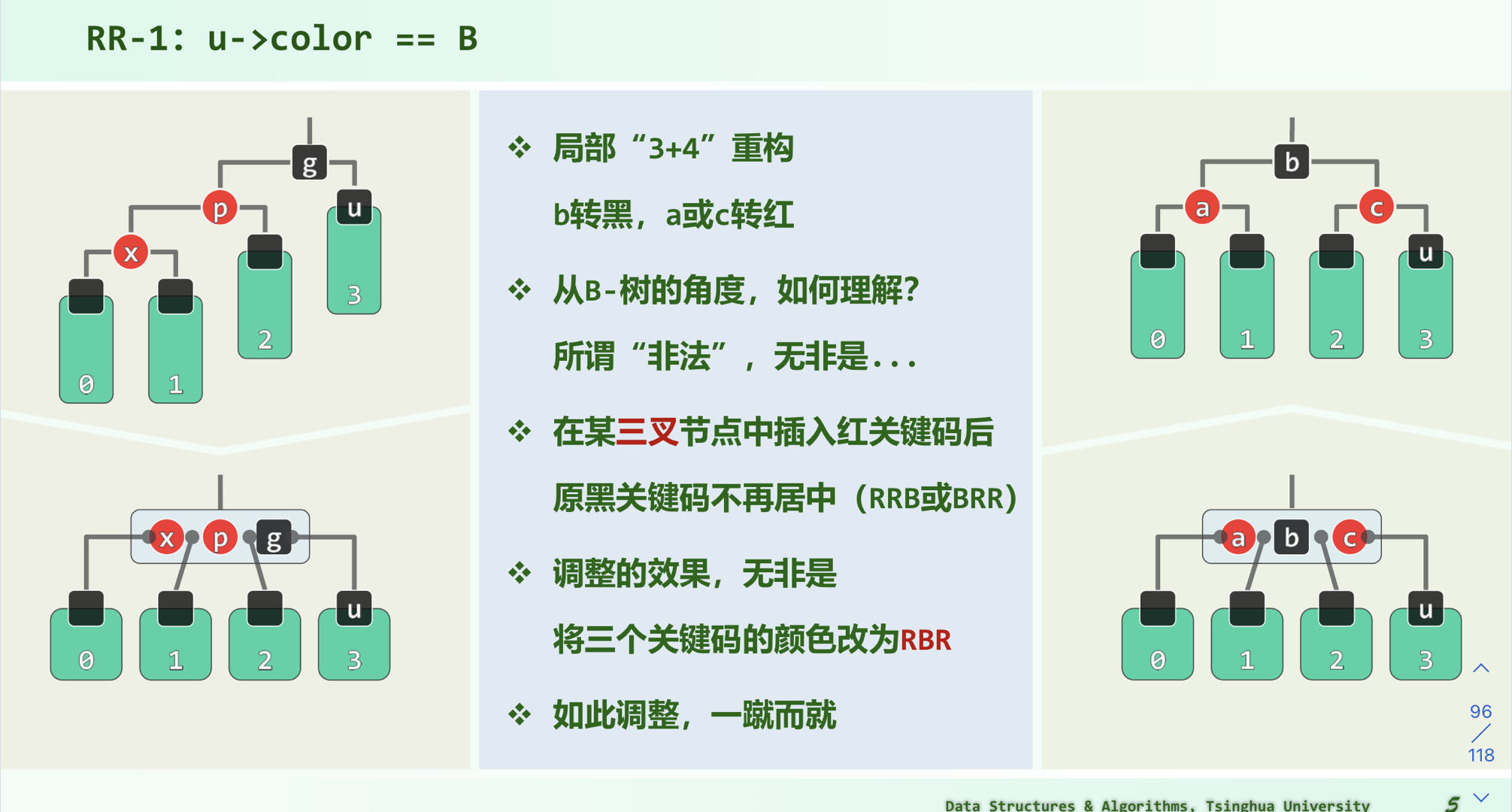
经过3-4重构之后，将中间节点染黑，子节点染红

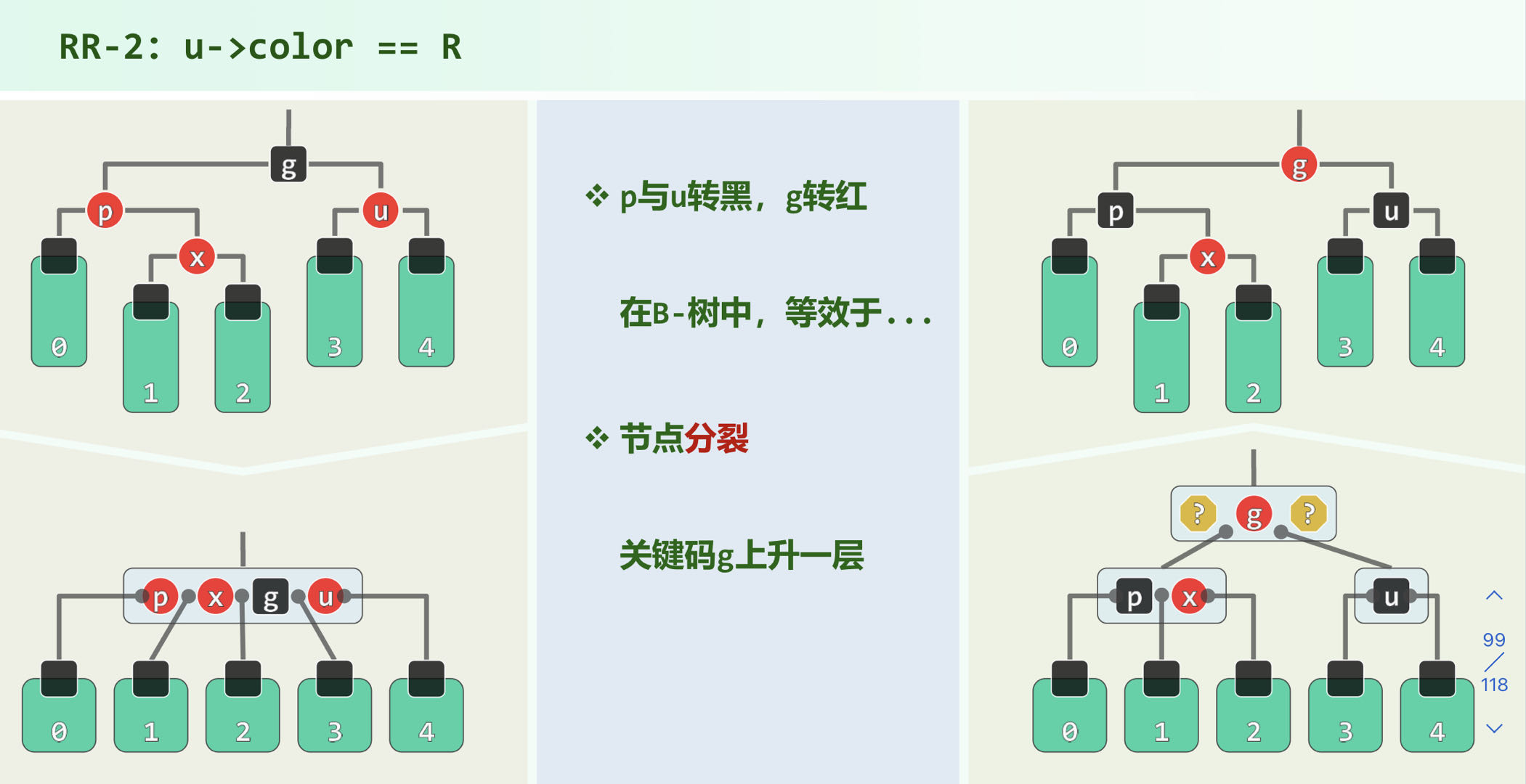
相当于B树上溢，将g染红上升1层，然后将p, u染黑

这样可能引起双红向上传播，则逐层实施双红解决策略

复杂度

$O(logn)$次重染色

$O(1)$次旋转（旋转过后必然全局恢复）

删除

按照原BST删除操作删除，3、4规则可能会违反

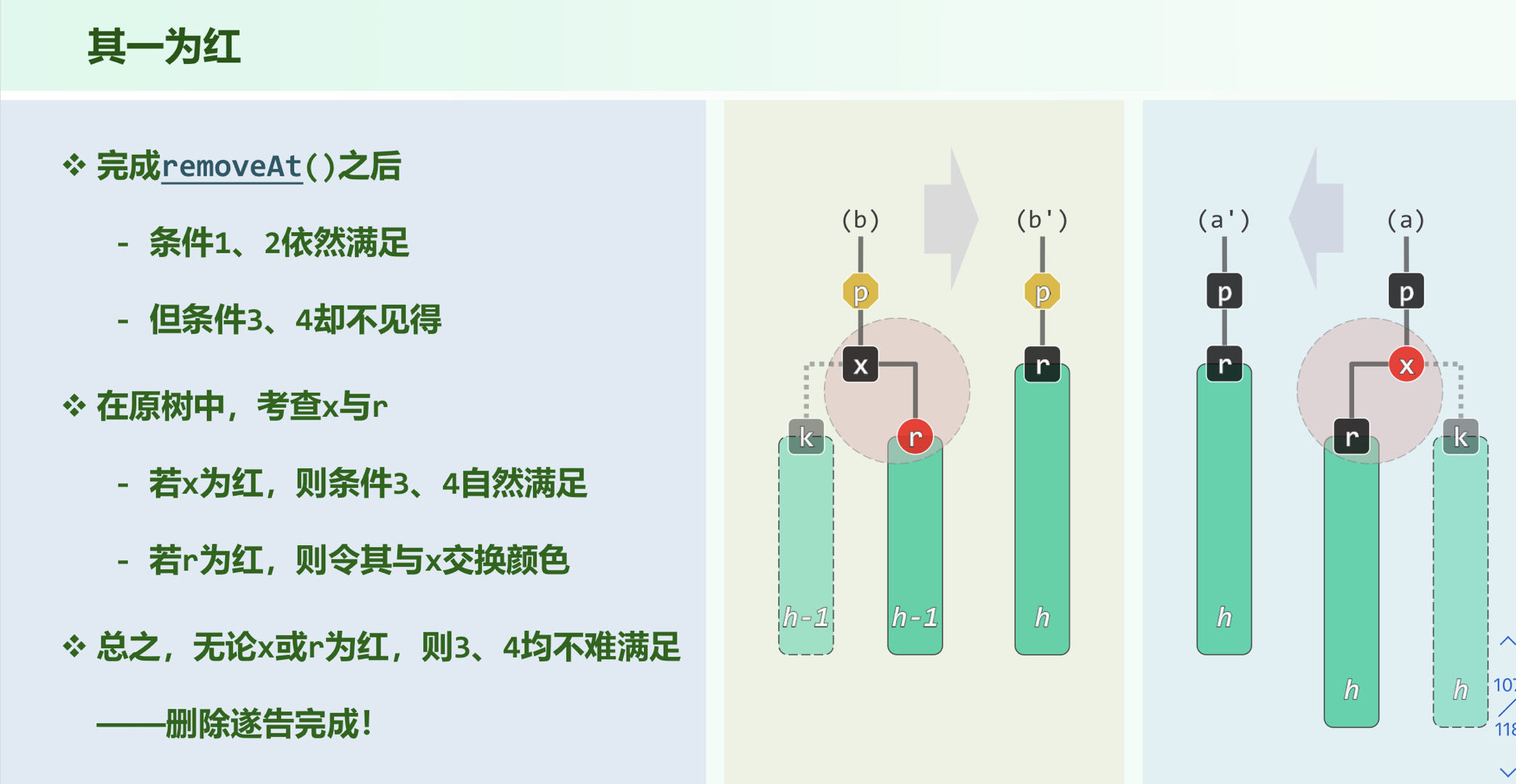
双黑

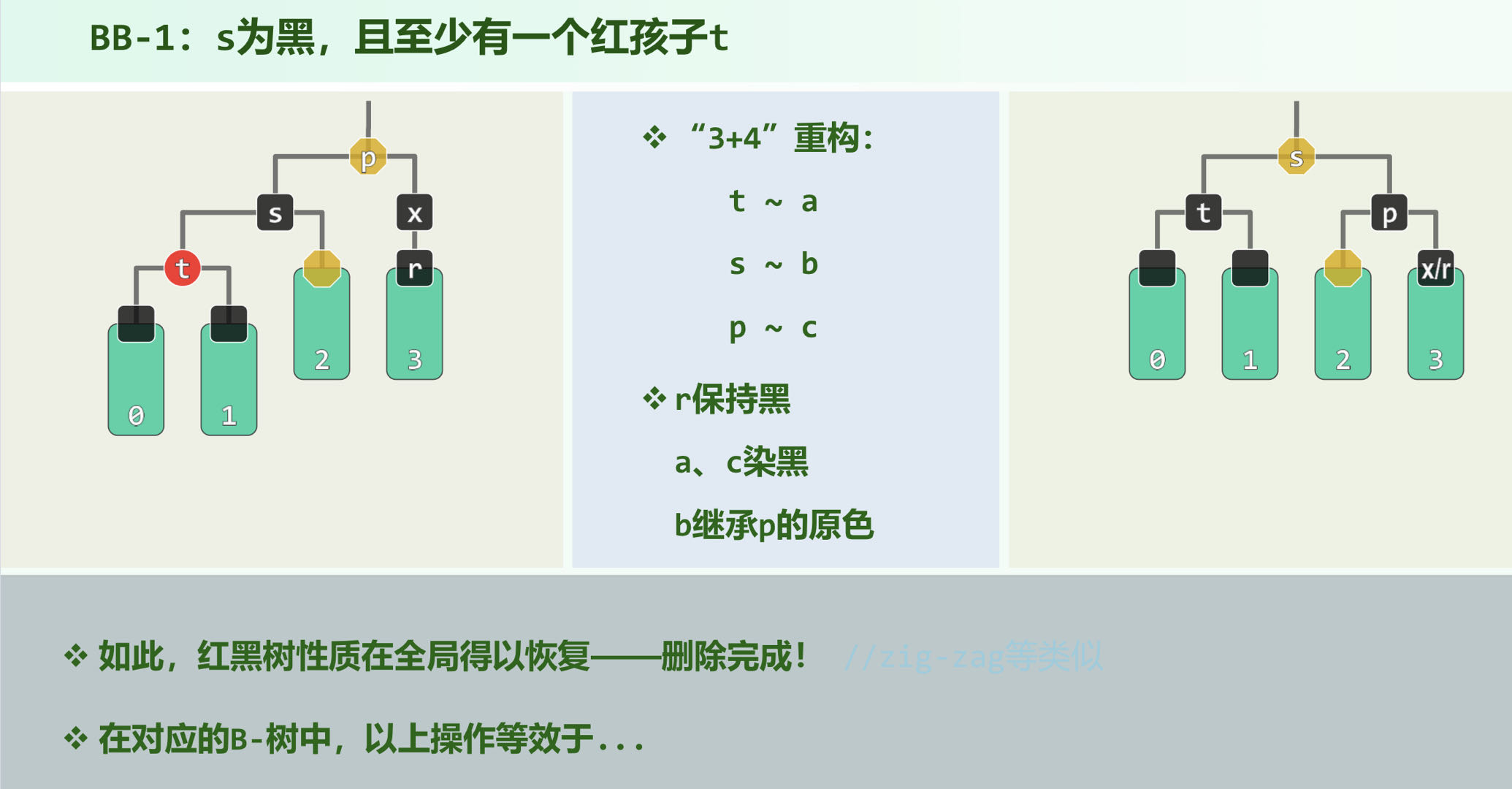
3-4重构

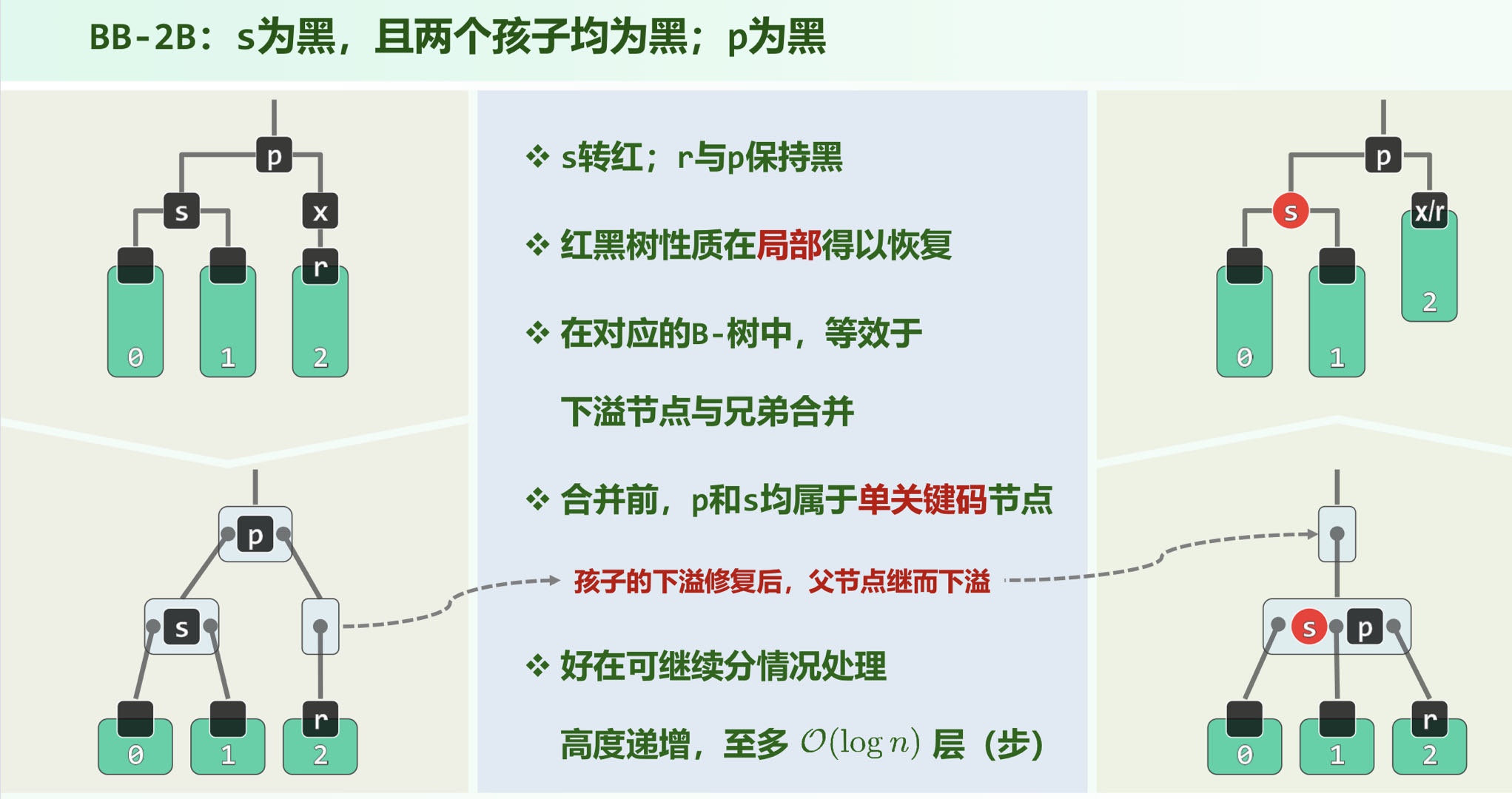
局部修复之后，父节点会下溢，仍然可以看成原父节点是个黑节点，从而进行双黑修正

复杂度

$O(\log n)$次重染色

$O(1)$次旋转（旋转过后必然全局恢复）

红黑树考前再看看！！