PS-07 Search Tree Application

1. Range Query

1-D

将所有点组织成一个有序的向量，通过二分查找找到最右的边界，然后反向report，这样的复杂度是 $O(logn+r)$， $r$是report所需的固定时间无法优化

2-D

点分布在二维平面上，用上闭下开，右闭左开的区间去框住

2. K-D Tree

2-D

先递归地划分区域

找到中间点，奇数层竖直划分，偶数层水平划分，划分区域为右上闭，左下开

最终K-D树为 $logn$层

Quadtree

将区域四等分四等分的划分，但是可能会出现空的区域

Query

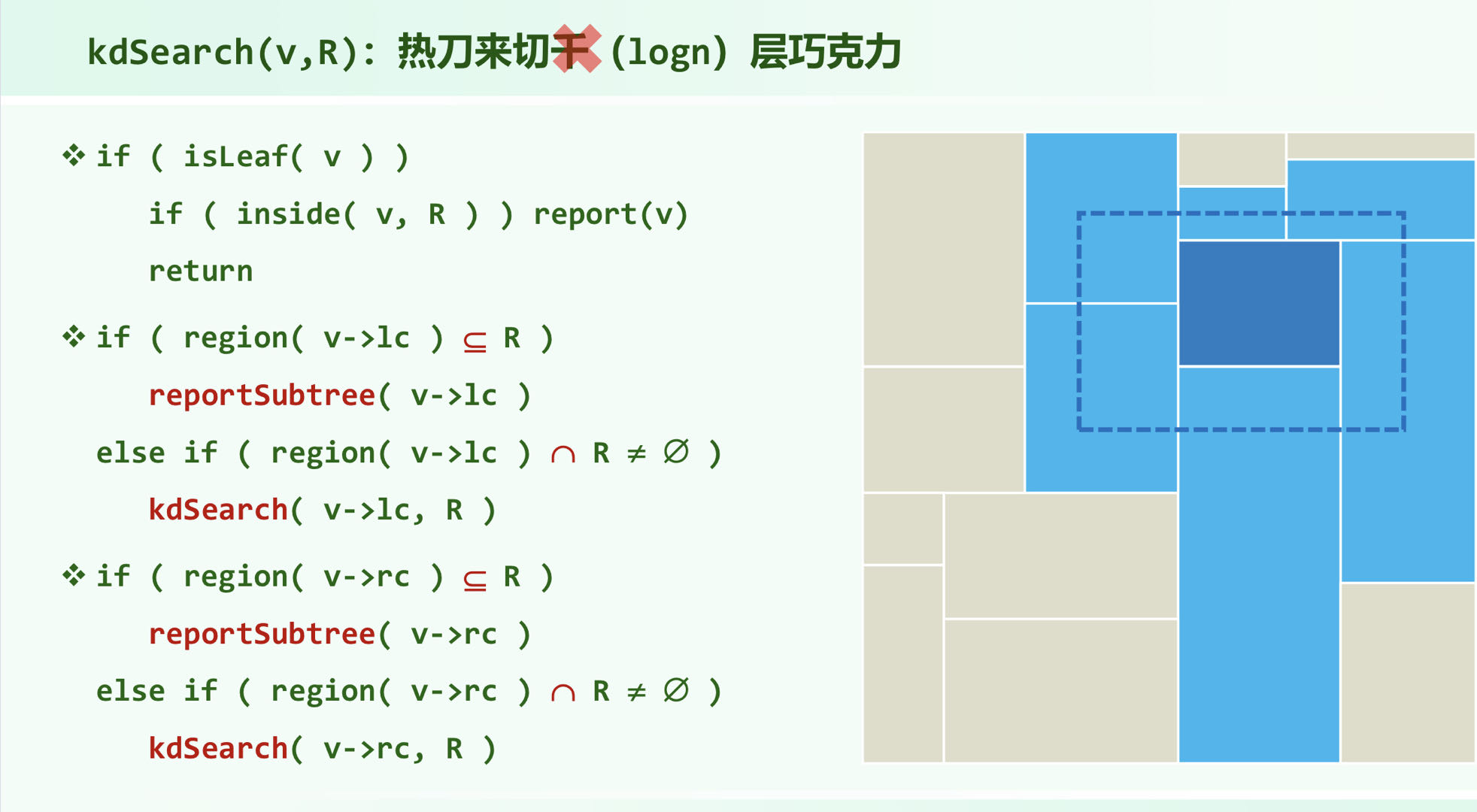
复杂度

构建K-D树的时间复杂度为 $O(nlogn)$

空间复杂度为 $O(n)$

查询复杂度为 $O(\sqrt{n}+r)$为什么？？？

3. Interval Tree（区间树）

在一个区间的集合中找到包含一个点的所有区间

首先找到所有端点中最中间的那个点，以这个点做划分，包含这个点的留下，在这个点左边的区间放到左孩子中，在这个点右边的区间放到右孩子中，然后递归地生成Interval tree

深度

左右孩子中的区间数都 $≤n/2$，全树的高度必然为 $O(logn)$

节点存储方式

用两个列表分别存储每个区间的左端点和右端点，左端点按从小到大排列，右端点按从大到小排列

查询

对每一个查询点，和每个节点中分割中点比较，假设大于中点，则对右端点从大到小比较，如果查询点在对应区间中，则report，再递归查询右子树；如果查询点等于中间分割点，则直接report该节点

4. Segment Tree（线段树）

同样的目的，但是以所有区间的端点作为分割点分割整个数轴，得到 $2n$个线段，在每个线段中存储包含这个线段的区间，这样组成的树为线段树

但如果分割地过于细致会导致空间复杂度过大为 $\Omega (n^{2})$

考虑将两个存储在相同父亲节点的两个孩子中的属于同一区间的线段合并，最终所有区间的存储空间为 $O(nlogn)$为什么？？

查询时间为 $O(logn)$