PS-14 Sorting + Selection

1. 快速排序

策略

找到一个轴点，然后将元素与轴点比较，小的放在左边，大的放在右边

轴点：在本来有序向量中所属位置的点

但轴点不是一开始就有的，因此我们要培养轴点

快速划分：LUG版

随机的选取候选者，比如 $elem[0]$，然后由 $lo$到 $hi$，交替向内移动，先从 $hi$开始比较，有小于轴点的即转到 $lo$，如此反复，各元素最多移动1次，因此划分只需 $O(n)$的时间

一般在选取候选者时有一步随机的交换，目的是使原本不随机的序列变得随机

递归深度

此算法所需额外空间仅为 $O(1)$，但没考虑递归的深度，递归深度可能会有最坏的情况达到 $O(n)$，

但是概率非常非常低，期望来讲大概率还是 $O(logn)$，因此我们认为该算法还是就地的

迭代

或者也可以采取迭代的办法，大任务先入栈，小任务后入栈，需要的辅助栈空间也不过 $O(logn)$

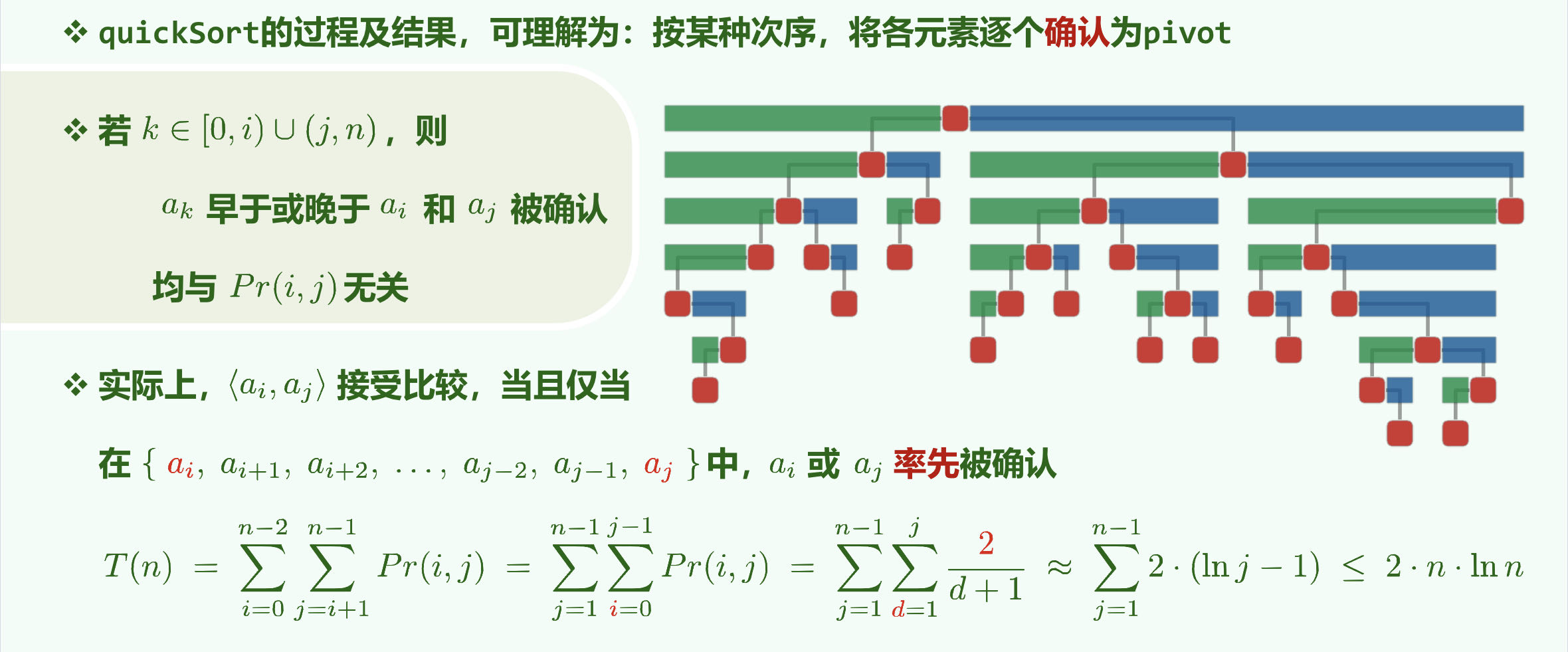
比较次数

$T(n)=(n-1)+\frac{1}{n}\sum_{k=0}^{n-1}[T(k)+T(n-k-1)]=(n-1)+\frac{2}{n}\sum_{k=0}^{n-1}T(k)$

经过一系列化简

$\frac{T(n)}{n+1}-\frac{T(n-1)}{n}=\frac{4}{n+1}-\frac{2}{n}$

经过累加法得

$\frac{T(n)}{n+1}\approx 2\ln n$

$T(n)\approx 1.386\cdot nlogn$

也可以采用后向分析的方法：

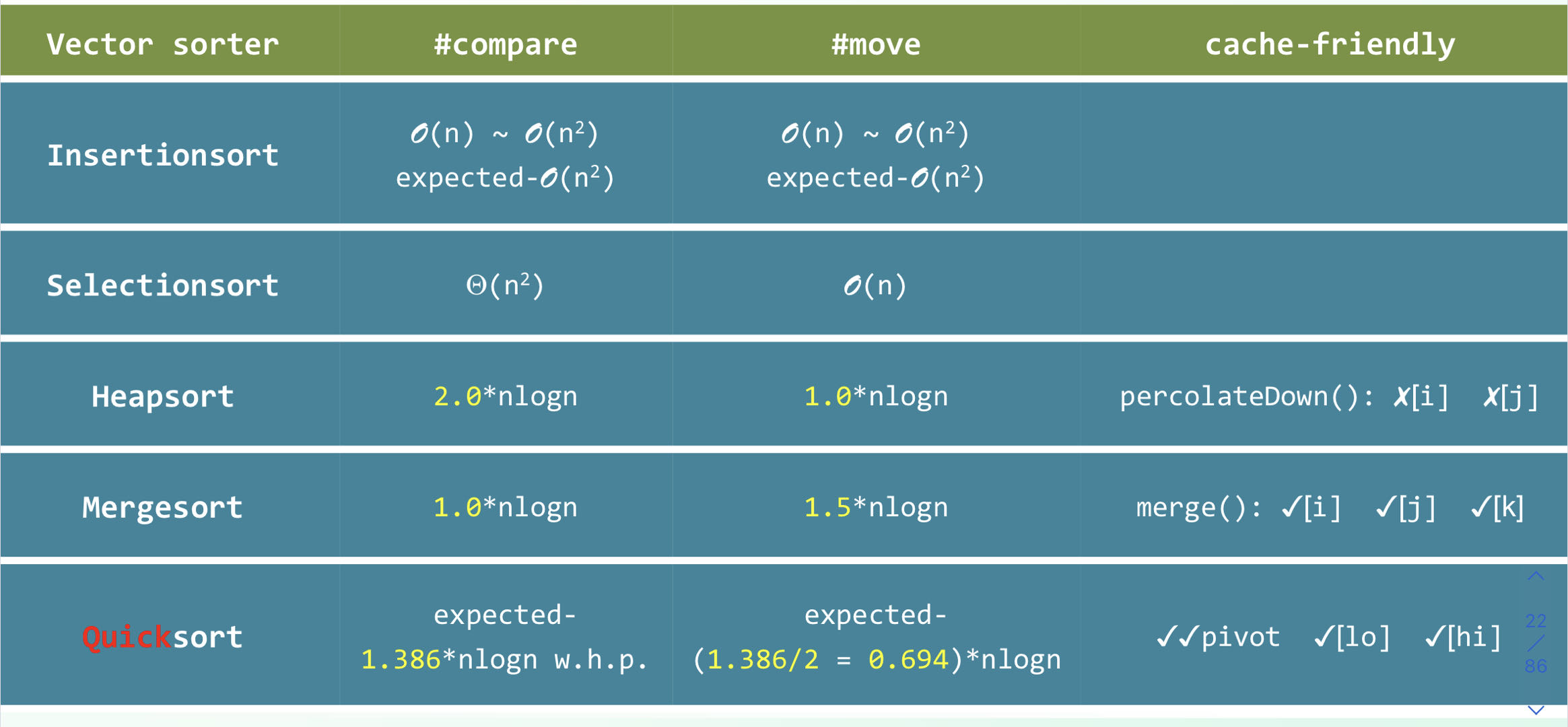
几种排序算法对比

快速划分：DUP版

大量元素重复时，会导致划分的失衡，使得递归深度过大，DUP版将原算法中比较的等号去掉，这样可以缓解失衡的问题，降低递归的深度

快速划分：LGU版

顺序遍历元素，逐一和轴点比较，less则放在序列的L部分（实则是和G中第一个元素交换），greater则不需要移动，直接继续拓展，是非常简单的一种算法

以上算法都存在不稳定的问题

2. 选取

QuickSelect

经过反复地做quicksort中的partition操作，最终选出第k大的元素

期望的复杂度为 $O(n)$，但仍存在最坏情况！

LinearSelect

3. 希尔排序

相隔一定步长的插值排序，步长按特定的序列从大到小变化