PS-04 Stack + Queue

1. 栈的接口与实现

栈只能在栈顶插入和删除，后进先出

• 接口
  • size() / empty()
  • push()
  • pop()
  • top()

2. 栈的应用

函数调用栈

递归算法所用的空间主要取决于递归的深度，而不是递归实例的总数（因为递归实例并不是同时出现，每层递归只调用一个递归实例）

尾递归

当每次递归只出现在最后一步时，这个递归就可以消除，时间上会有常系数的改进，空间上会大幅度改进

进制转换

短除法，反复整除留余

要找到一种算法，可以自低而高的保留数位，然后自高而低的输出

栈就是这样一种满足要求的数据结构

括号匹配

分治策略和减治策略是不可行的，他们只满足充分条件，不满足必要条件，这是一种由外而内的策略

思考一种由内而外的策略，从内部一点一点将紧邻的括号消去从而判断是否全局匹配，要想实现这种策略，可以考虑使用栈

栈混洗

考察栈 $A,B,S$，只存在 $S.push(A.pop()),B.push(S.pop())$两个操作

可以考察 $S$再度变空 $n$种情况，实际上就是对 $A$中除第一个元素外（因为第一个元素必然排在 $k$个元素的末尾）前 $k-1$个元素栈混洗再对后 $n-k$个元素栈混洗

因此最后得到的组合数为

$SP(n)=\sum SP(k-1)\cdot SP(n-k)=catalan(n)=\frac{(2n)!}{(n+1)!\cdot n!}$

检测禁形

对任何 $1≤i<j<k≤n,[…,k,…,i,…,j,…>$，必然不是栈混洗

即不存在“312”的模式

括号匹配

$S$经历了n次push和n次pop正好对应n对括号的匹配，所以n对括号匹配的排序数量也是卡特兰数

中缀表达式求值

要先按照规则约定一个优先级，还要考察括号优先级

逆波兰表达式

不使用括号，即可表示带优先级的运算关系，也可以称为后缀式

用一个栈，遇到数就压入，遇到算符就弹出计算，更方便（好像）

中缀表达式与逆波兰表达式转换

将中缀表达式的每一次运算都用括号括起来，然后按照左括号和数字向下，运算符向上的规则写成一个起起伏伏的序列，这样每一个运算符都在同一高度上对应着一个右括号，然后将运算符移动到右括号对应的位置替换掉右括号，最后再落到同一排，转换就完成了

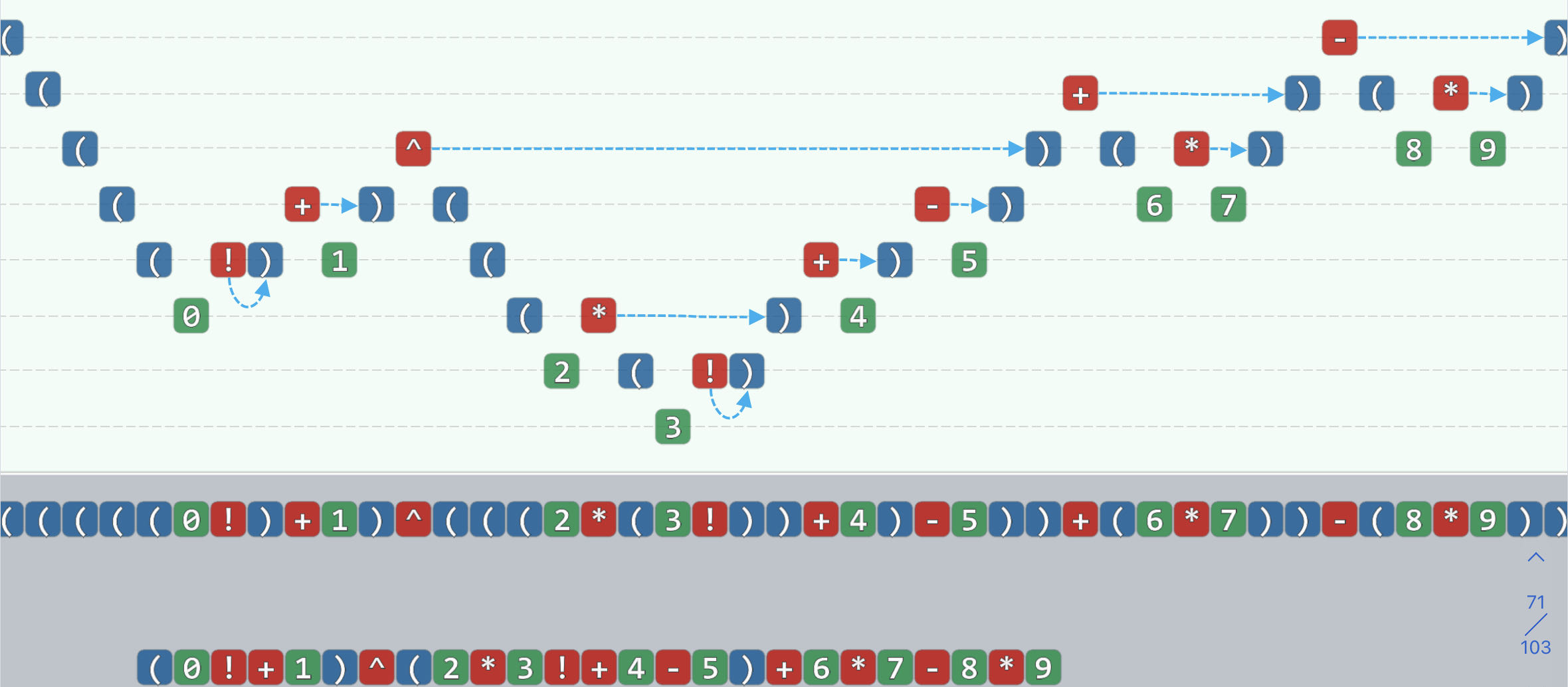
3. 队列的接口与实现

队列只能在队尾插入，从队头删除，先进先出

• 接口
  • enqueue()/rear()
  • dequeue()/front()

4. 队列应用

直方图内最大矩形

蛮力算法(Brute force)

逐一扫描选取最大的，复杂度 $O(n^{2})$

优化算法

对每一个直方矩形，找到它的左边界和右边界存起来即可，在找的过程中要进行适当的剪枝

5. 栈与队列

Steap = Stack + Heap

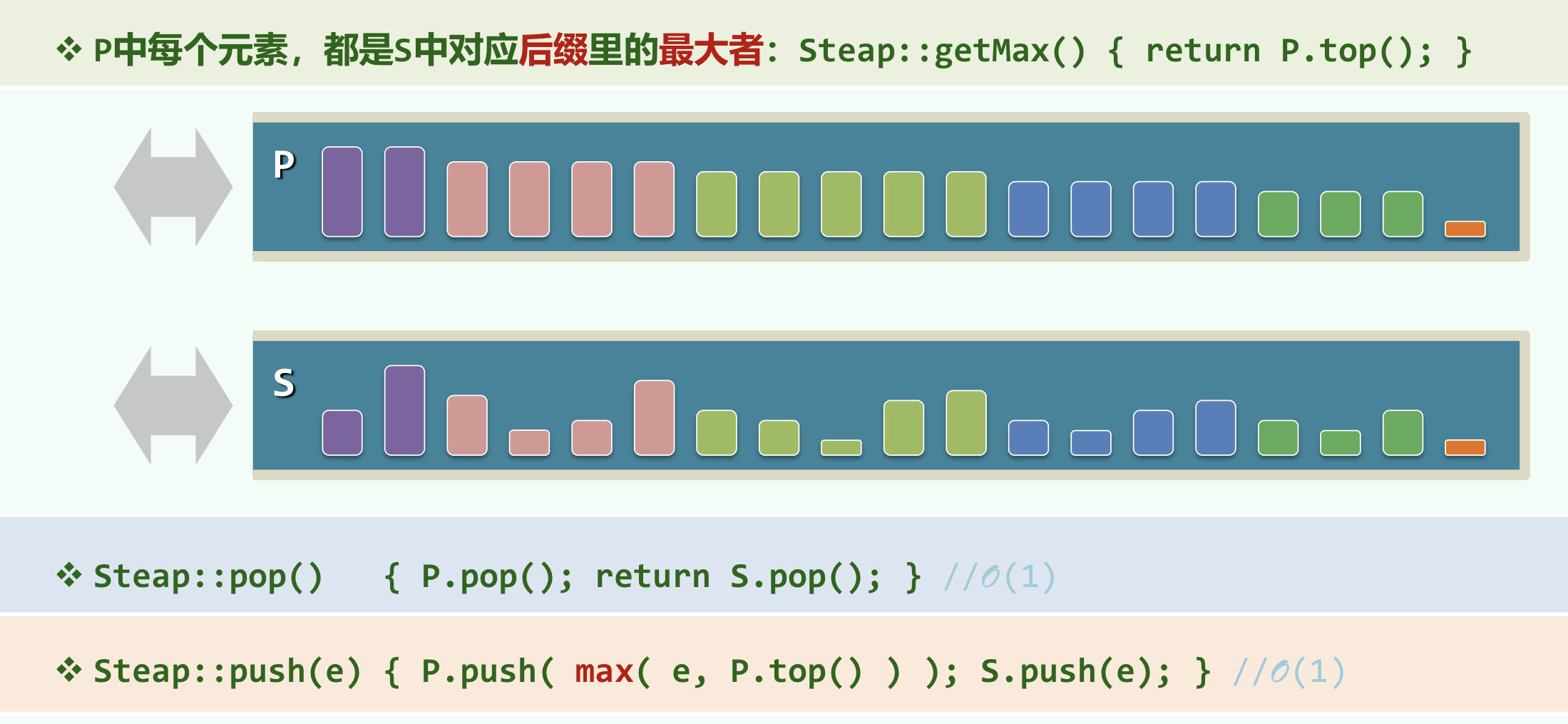
这样可以快速得出栈中最大的元素，但是 $P$中存了大量重复的元素似乎有些浪费空间，可以对其进行适当的简化：

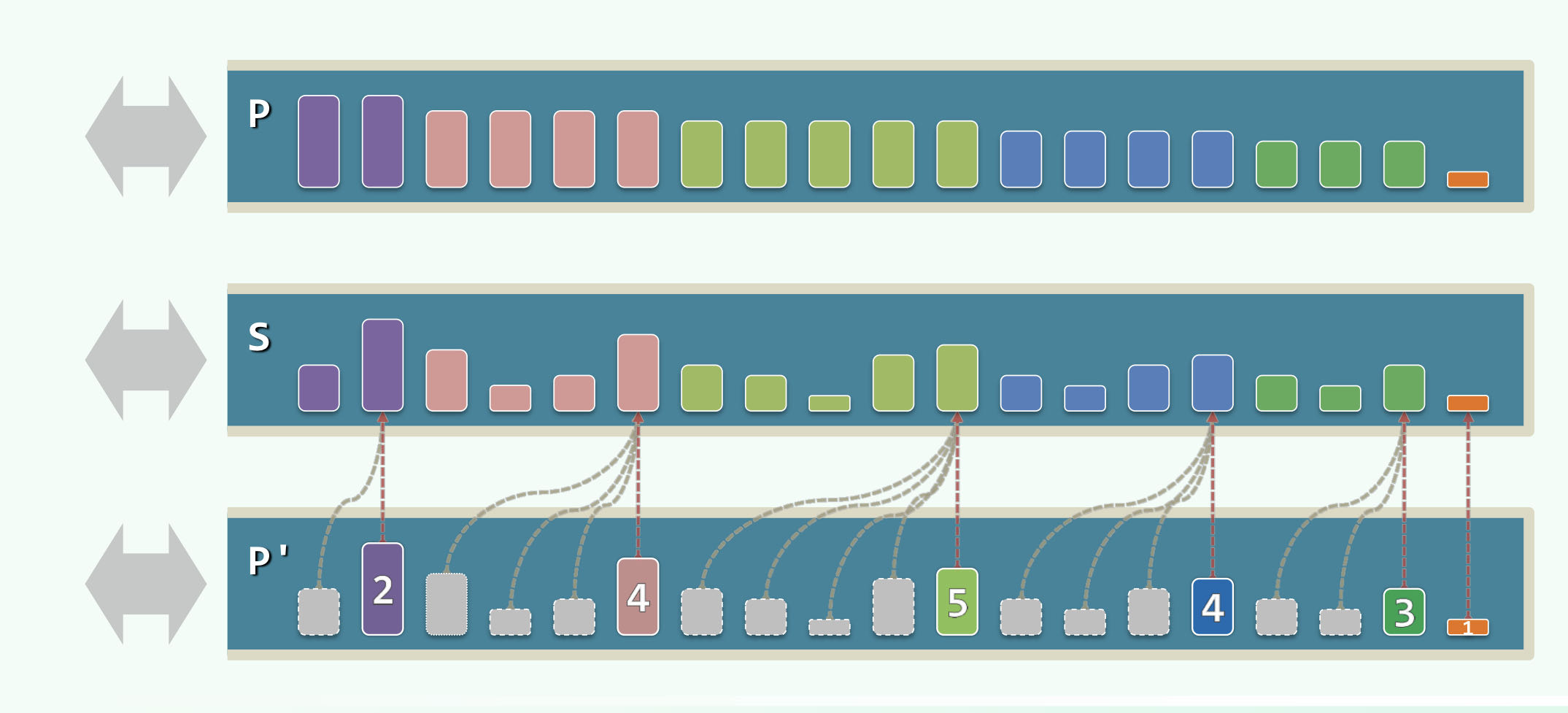
用压缩的方法，每个最大值部分存一个计数器，来了pop一个就-1，来更大的就push一个

Queap = Queue + Heap

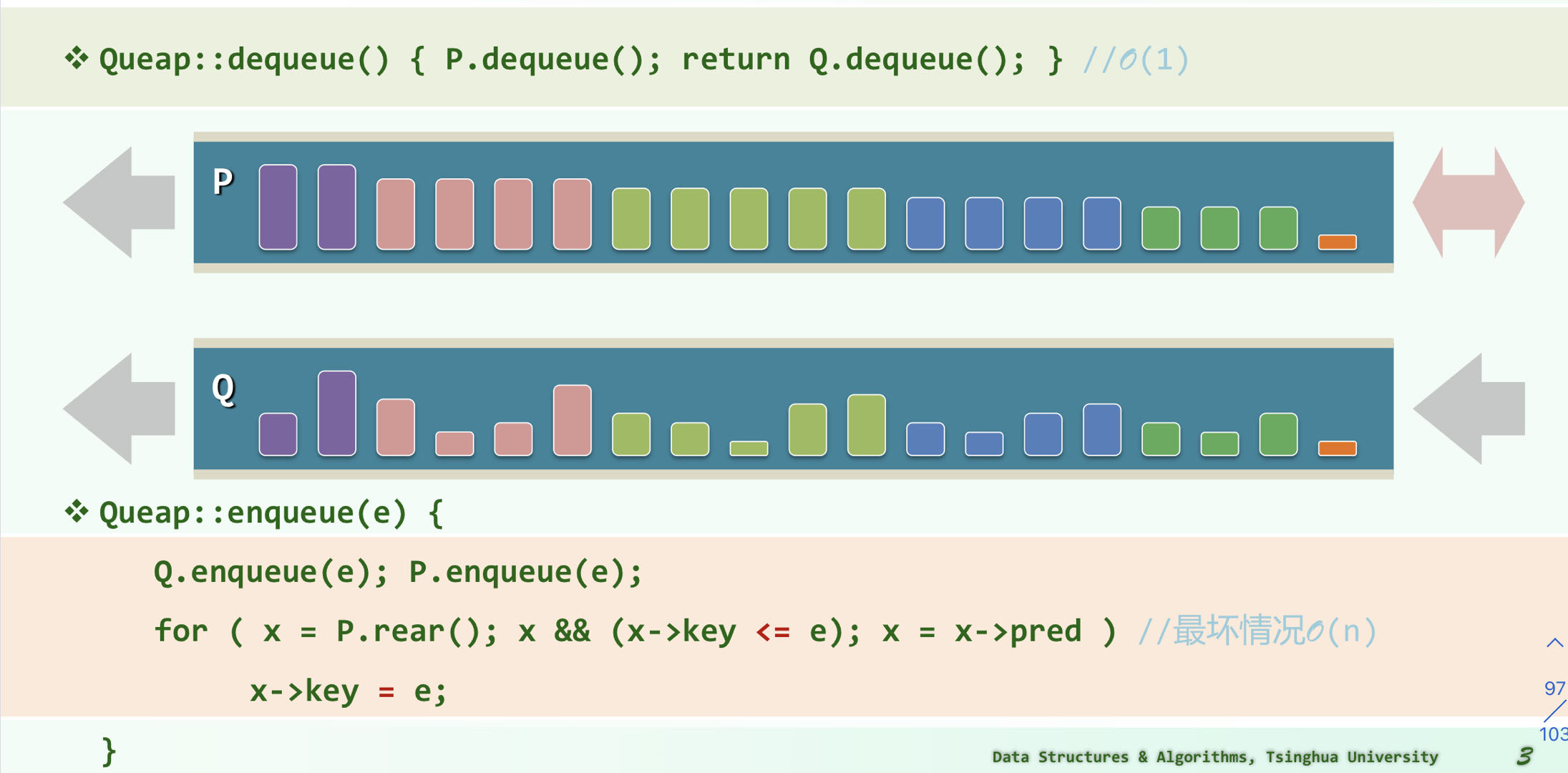
用队列时，更新复杂度就会变高，因为插入是从后缀插入， $P$要更新后缀的最大值

同样的也可以用压缩的方法降低空间复杂度

为什么 $P$的后缀可进可出？

双栈当队

复杂度分析

• Accounting

思考每个元素要进行的操作数，无非入栈、出栈、再入栈、再出栈四种 $O(1)$操作，因此分摊复杂度是 $O(4)$，这个以元素为研究对象

• Aggregate（校长算总账）

考虑队列是个学校，所有入过学的总数为 $e$，所有毕业的总数为 $d$，总共所花时间无非 $≤4d+3(e-d)$，则每次操作的分摊复杂度为 $\frac{3e+d}{e+d}<3$，这个以操作为研究对象

• Potential（势能）

很玄学的一个东西