PS-02 Vector

1. 从数组到向量

寻秩访问

其实就和数组一样…

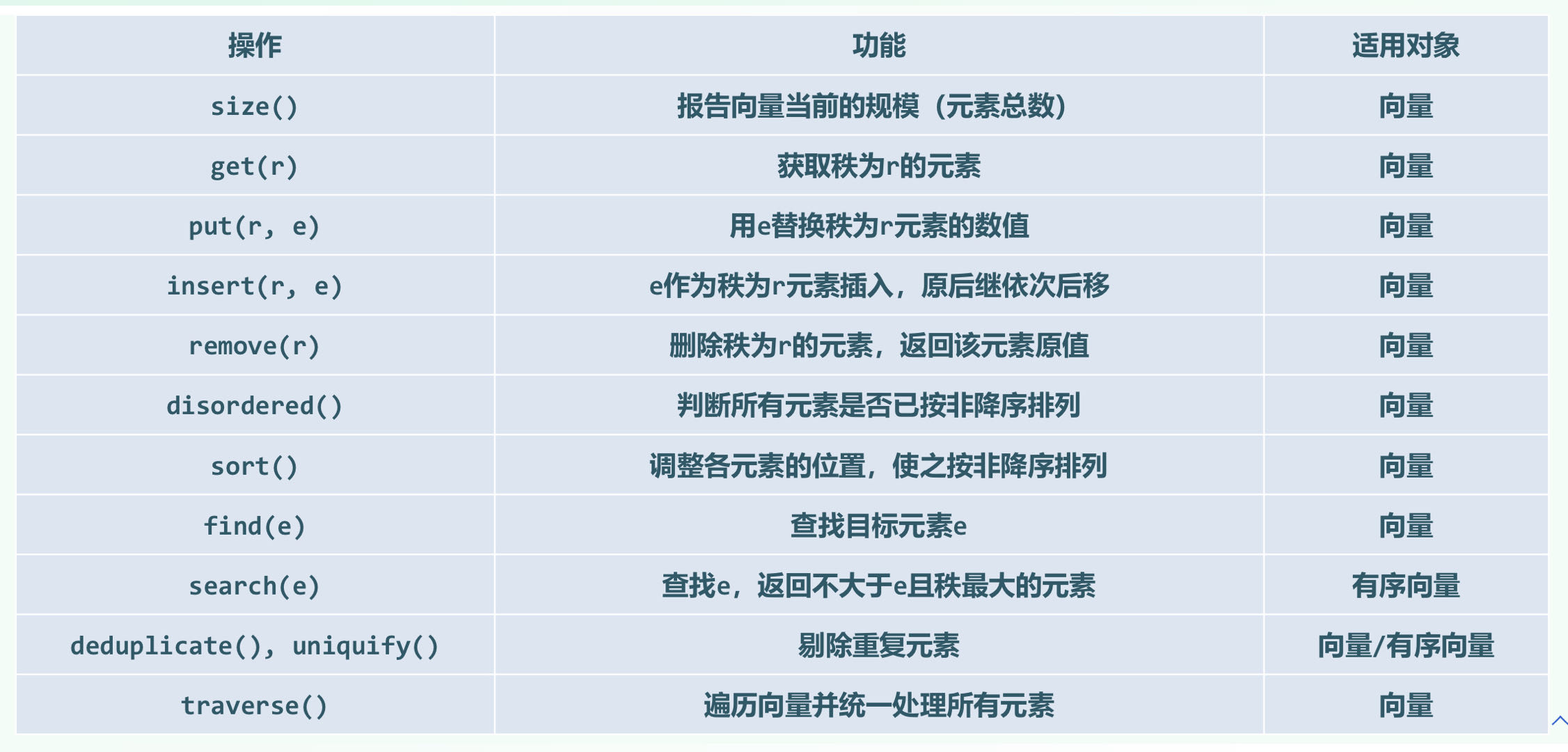
向量ADT接口

可扩充向量

开辟内部数组并使用一段地址连续的物理空间

$capacity$：总容量

$size$：实际规模

静态管理时容易出现 $size>capacity$或 $size\ll capacity$的情况，以至上溢或者下溢，因此需要动态调整容量

动态空间管理

在即将上溢时，将向量的容量加倍，注意还需要将原来向量的元素迁移到新的向量中，时间复杂度为 $O(n)$

(但是这种情况并不是总是发生的)

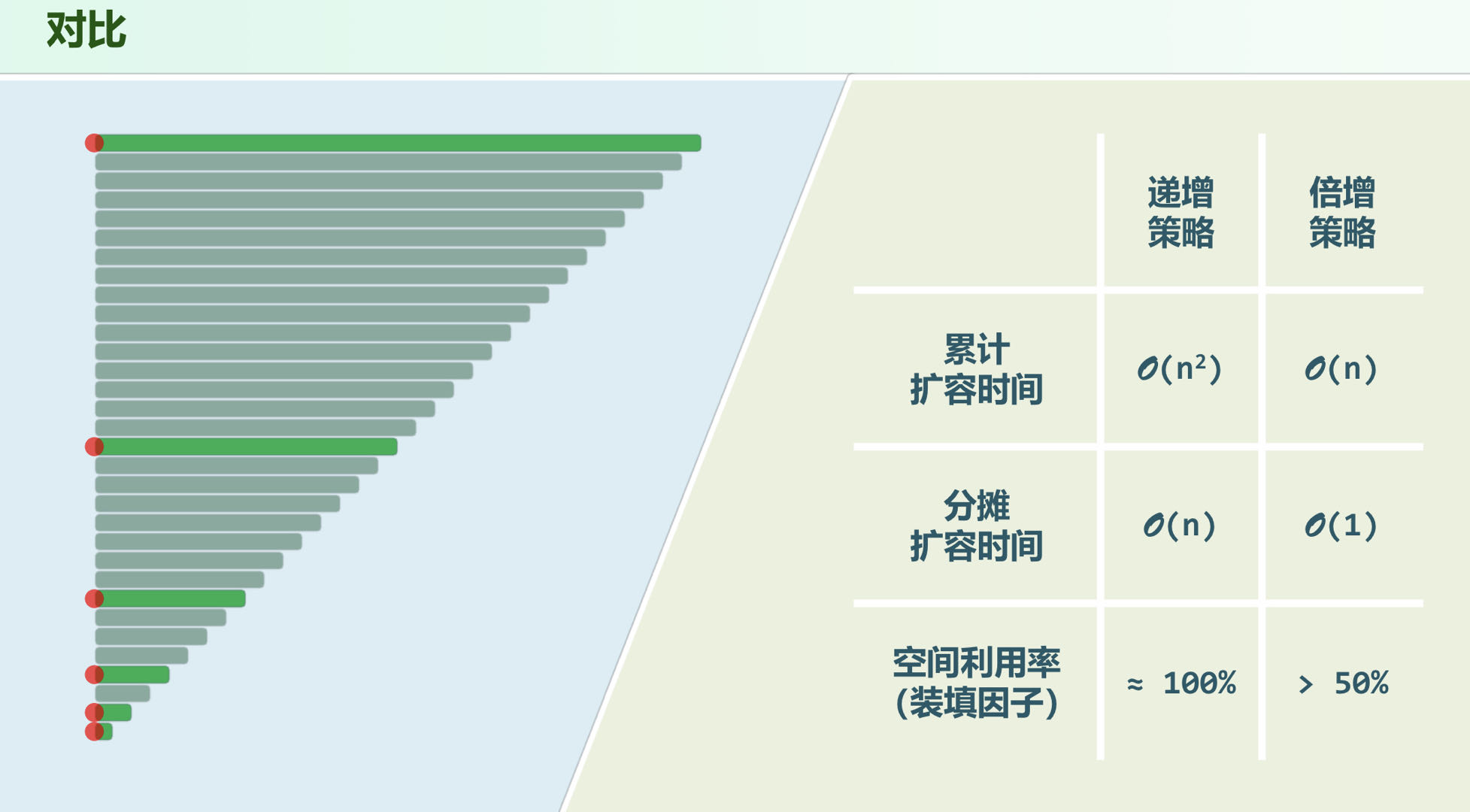
分摊分析

每次扩容过程所需时间的加和= $1+2+4+…+2^{m-1}$是几何级数，最终复杂度为 $O(n)$，但分摊到 $n$次扩容中去，复杂度不过是 $O(1)$的

思考：如果不采取容量加倍策略，其他的扩容策略比如递增策略是否可行？

如果采取递增策略，扩容所需时间是算数级数 $O(n^{2})$，分摊后为 $O(n)$

2. 无序向量

基本操作

• 插入：先扩容or not，然后插入
• 删除：先写区间删除的操作，单元素删除时调用区间删除

查找

一种基于比较和判等的查找方法（与后面要学的哈希表的查找方法不同）

从后向前比较，输入敏感，复杂度 $O(n)$

去重

去重，从头开始，拿出一个位置的元素向前查找，找到则删除，复杂度为 $O(n^{2})$

遍历

3. 有序向量

无序向量处理为有序向量之后相关算法可优化

唯一化

• 低效算法：从前向后逐一比对，相同则删除，但是删除算法本身的复杂度就是 $O(size-i)$，因此该方法很低效。此时向量已经是有序的了，重复的元素都聚集在一起，可以思考批量删除的方法。
• 高效算法：使用两个索引 $i,j$， $j$一直向前试探， $i$留在原地不动，当 $elem[i]≠elem[j]$时，把 $j$对应的元素丢到前面来，这样就完成了一批删除操作。

查找

二分查找（版本A）

分为了三种情况， $[lo,mi),[mi],[mi+1,hi)$，时间复杂度 $O(logn)$，这种方法的缺点是每次循环可能要比较两次，且数据类型比较所花的时间可能会比较长

成功、失败时的平均查找长度均大致为 $O(1.50\cdot logn)$

二分查找（版本B）

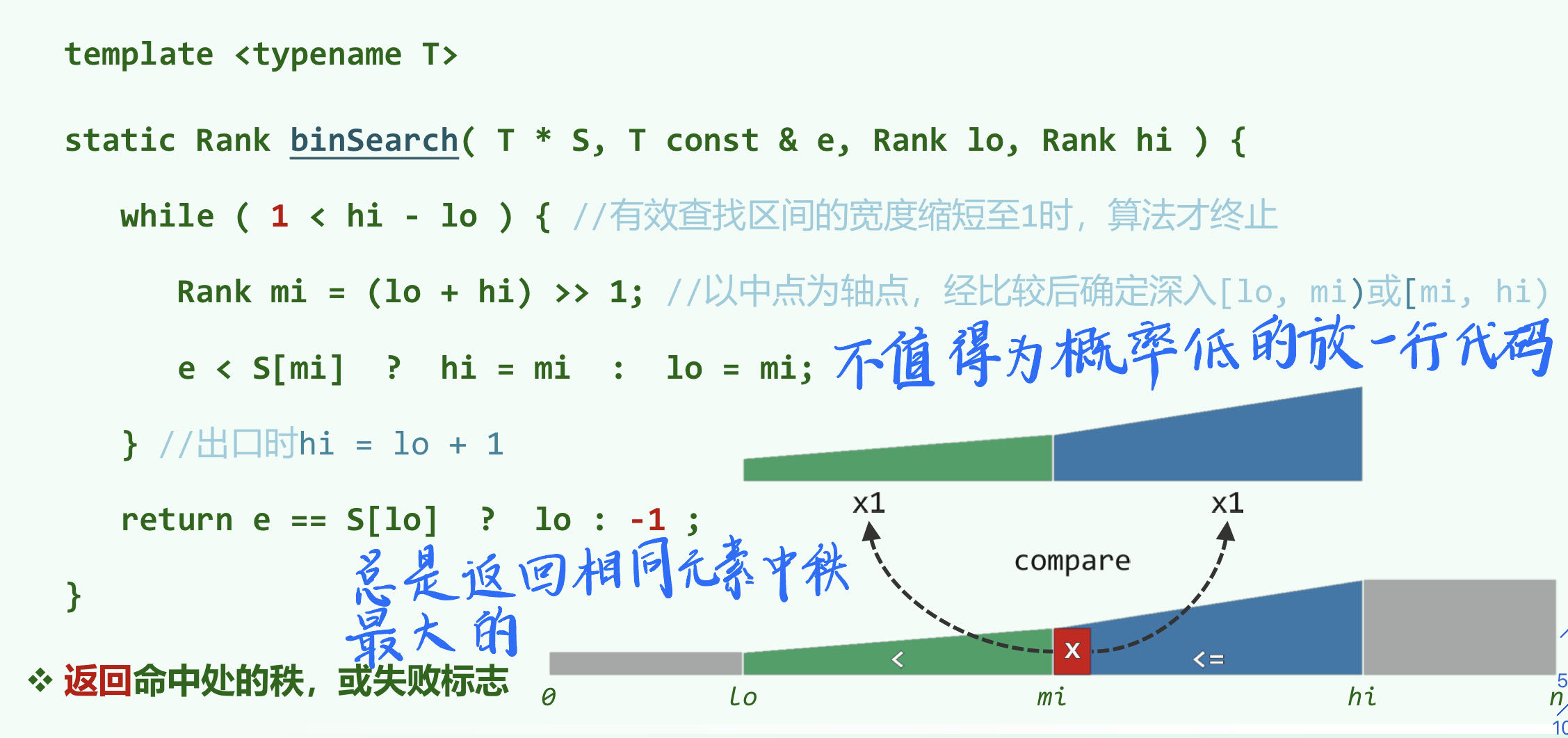
相比于版本A，版本B每次迭代少了一次比较，分为两种情况 $[lo,mi),[mi,hi)$，但迭代的深度必然达到 $logn$。相比版本A，最好(坏)的情况下更坏(好),性能更均衡

但是为了维护向量的有序性（即使查找失败也要给出适当的位置）和稳定性（重复元素也要按照插入次序排列），还需要查找算法在目标不存在时和目标存在多个时都返回一个有效的秩

约定总是返回小于等于查找元素 $e$的元素的最大的秩，为此还需更好的实现方式！

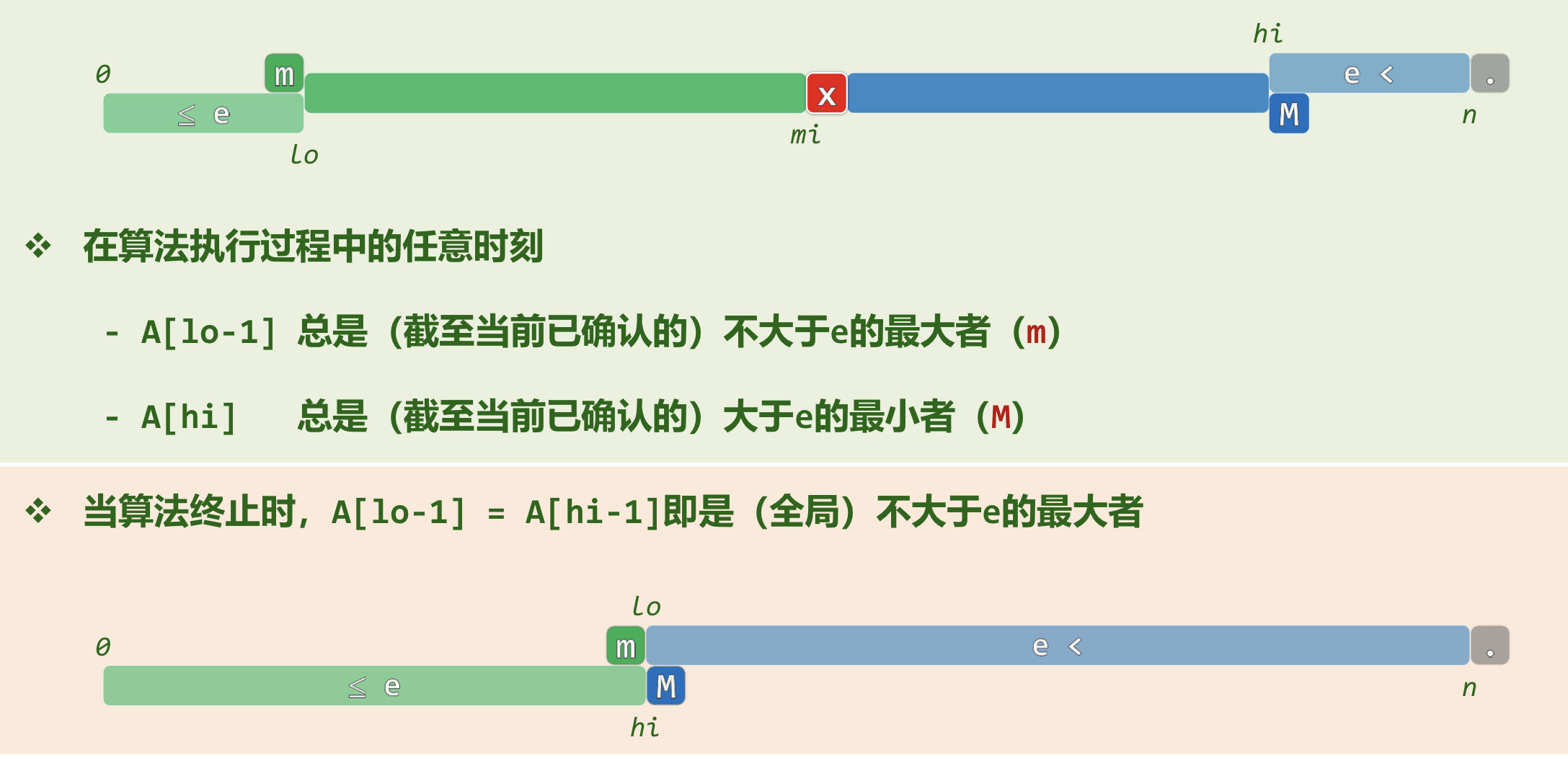
二分查找（版本C）

这个方法在每次迭代的过程中，大胆地跳过了 $S[mi]$，但这种方法是能满足要求并且非常正确的！

从循环不变性的角度来看， $A[0,lo)≤e<A[hi,n)$， 在已知的范围内，$A[lo-1]$总是目前不大于e的最大者， $A[hi]$总是大于e的最小者

插值查找

当数据量足够庞大时，数据近似呈线性分布，因此可采取线性的插值方法来插入元素

（数据的分布可能不是线性，但依然可以按照其他规律来插值）

性能： $O(loglogn)$为什么？？？（有待求问）

在数据范围很大时，插值查找有明显的优势，但数据量不是非常大时，优势也不是很明显，引入了乘法除法运算反而不好

实际可行的方法：

• 先插值查找缩小数据范围
• 再二分查找进一步缩小范围
• 最后顺序查找

排序

• 起泡排序
• 选择排序
• 归并排序
• 堆排序
• 快速排序
• 希尔排序

起泡排序

依次比较每一对相邻的元素，如果逆序则交换之，反复扫描，直到确认顺序

提前终止版：

经过反复扫描之后，有可能前缀就已经有序了，这时就不用再扫描了，可以提前终止

跳跃版：

有可能后缀已经有序了，每次扫描的终止位置可以提前

以上起泡排序算法都是稳定的

归并排序

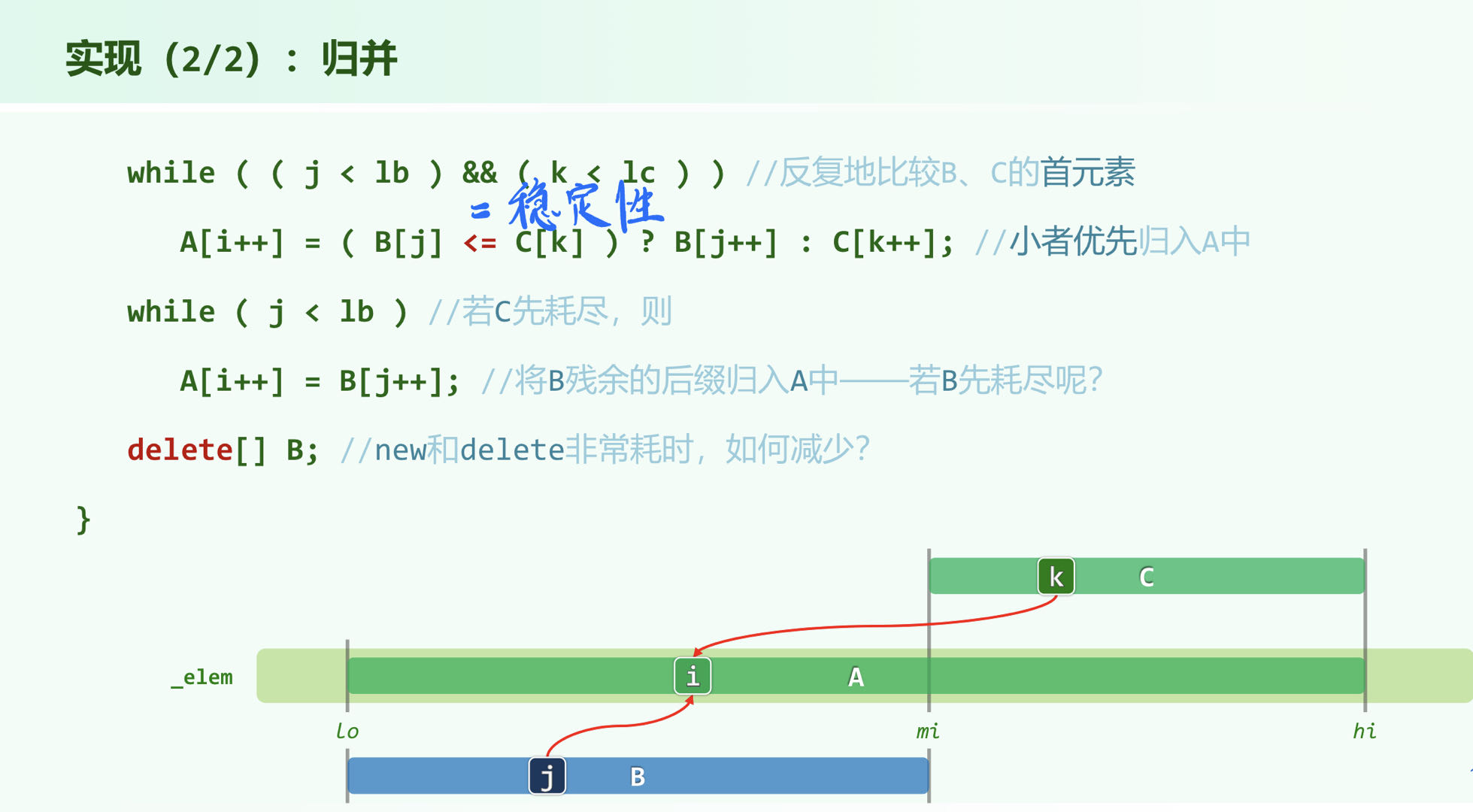
复杂度： $O(nlogn)$

4. 位图（bit map)

一种针对有限整数集的数据结构

取一段连续的存储单元（bit），如果元素存在，则相应位置的bit置为1，否则为0

可实现去重和排序，复杂度均为 $O(n)$