PS-01 Introduction

1. 计算：算法

算法

定义：在特定计算模型下（例如：计算机），旨在解决特定问题的指令序列

• 特点：
  • 正确性：可以解决指定的问题
  • 确定性：描述为基本操作组成的序列
  • 可行性：每一个基本操作都能实现，并且是在常数时间内完成的
  • 有穷性： 对于一个特定问题都可以经过有限次基本操作解决

Hailstone序列

$Hailstone(n)=\begin{cases}\{1\}&n \leq 1\\\{n\}\bigcup Hailstone(n/2)&n=even\\\{n\}\bigcup Hailstone(3n+1)&n=odd\end{cases}$

对任意的 $n$ ，Hailstone都能得到最终结果1，说明这个算法是有穷的，但还未在数学上证明

几何分布

$P(X=n)=(1-p)^{n-1}p$

$E(X)=\frac{1}{p}$

2. 计算模型：统一尺度

图灵机

为不同算法的代价的衡量提供一个统一的尺度，从而可以更好地评价算法的优劣

• 组成
  • Tape：一条纸带，被划分为无数个单元格，每个单元格上存储一个字符，表示该单元格的一个状态，每个单元格初始状态为 #
  • Head：每个时刻都对准某一单元格，可以对单元格内的字符读取或改写，并可以在下一个时刻转向左/右
  • Alphabet：每个单元格内的字符表
  • State：图灵机每个时刻都在某一确定的状态，当Head转入h时，停机

计算成本：从启动到停机所经历的转移次数

$(q, c; d, L/R, p)$表示当前状态为q，Head所在单元格字符为c；将当前字符改写为d，并在下一时刻向左/右转移，状态转变为p

RAM （Random Access Machine）

同样为评价算法的效率提供统一的尺度

例：Ceiling Division（向上取整除法）

思考：在TM、RAM等模型中衡量算法效率，为何通常只考查运行时间？空间呢？

主要是出于研究和分析的便利性考虑。这是因为对于许多算法来说，运行时间是最主要的性能指标，而空间复杂度往往与算法的时间复杂度相关，可以通过时间复杂度的分析间接得出。

3. 渐进复杂度

$T(n)=O(f(n))$渐进上界 $\exist c>0,s.t.T(n)<cf(n),\forall n\gg 2$

$T(n)=\Omega (f(n))$渐进下界

$T(n)= \Theta (f(n))$渐进确界

O (1)常数复杂度

$2023\times 2023=O(1)$，甚至 $2023^{2023}=O(1)$，从渐进的角度来看确实如此

一段代码是否为常数执行时间应具体分析！

• 代码中可能包含循环：

for(i = 0; i < n; i += n/2023 + 1) //2023,O(1)

分析：

假设 $2023k < n < 2023(k+1)$，则经过2023步循环之后 $i=2023(k+1)$必然大于 $n$，所以该循环是常熟复杂度的

• 代码中可能包含分支
• 代码中可能包含（递归）调用

O ( $log^{c}$n)多项式对数复杂度

复杂度无限接近于常数，非常好！

O ( $n^{c}$)多项式复杂度

线性复杂度 $O(n)$，通常就已经很不错了

O ( $2^{n}$)指数复杂度

NP-complete算法，无法忍受！！！

例如：subsetsum问题

注：O(nlogn)的算法最常出现，但不一定是最优，比如排序、Huffman编码（可以用桶排序在O(n)实现）

4. 复杂度分析

• 主要方法
  • 迭代（级数求和）
  • 递归（递归跟踪+递推方程）
  • 实用（猜测+验证）

级数

算术级数：与末项平方同阶 $T(n)=1+2+…+n=O(n^{2})$

幂方级数：比幂次高出一阶 $T(n)=\sum k^{d}=O(n^{d+1})$

几何级数：与末项同阶 $T(n)=a^{0}+a^{1}+a^{2}+…+a^{n}=O(a^{n})$

收敛级数：

$\sum \frac{1}{(k-1)k}=O(1)$

$\sum 1/k^{2}=O(1)$

$\sum \frac{1}{k^{2}-1}=O(1)$

调和级数： $h(n)=\sum 1/k=\Theta (logn)$

对数级数： $\sum lnk=\Theta (nlogn)$

对数+线性+指数： $\sum klogk=O(n^{2}logn)$

$\sum k\cdot 2^{k}=O(n\cdot 2^{n})$

迭代

具体问题具体分析…

封底估算

• 1天= $10^{5}$秒
• $2^{10}=10^{3}$

5. 减而治之(Decrease and conquer)

求解大规模的问题，可以：

• 将其划分为两个子问题，一个规模减小，一个平凡
• 分别求解子问题

递归跟踪

写出每一个递归实例，分别计算复杂度再求和

递推方程

根据一个问题和子问题的递推关系求其复杂度，例如 $T(n)=T(n-1)+O(1)$

6. 分而治之(Divide and conquer)

求解大规模问题吧，可以：

• 将其划分为若干个子问题，且规模相当
• 分别求解子问题

主定理

若递推关系式为 $T(n)=a\cdot T(n/b)+O(f(n))$

• 若 $f(n)=O(n^{log_{b}a-\epsilon})$，其实就是 $f(n)$阶数比 $n^{log_{b}a}$小， $T(n)=\Theta(n^{log_{b}a})$
• 若 $f(n)=\Theta (n^{log_{b}a}\cdot log^{k}n)$， $T(n)=\Theta (n^{log_{b}a}\cdot log^{k+1}n)$
• 若 $f(n)=\Omega (n^{log_{b}a+\epsilon})$， $T(n)=\Theta (f(n))$

7. 动态规划：记忆法

斐波那契数列

int fib(n){return (2 > n)? n: fib(n-1) + fib(n-2);}

这种递归方法非常慢，因为使用了大量重复的计算结果

采用动态规划迭代的方法， $T(n)=O(n)$

f = 1;    //fib(-1)
g = 0;    //fib(0)
while(0 < n--){
	g = g + f;
	f = g - f;
}
return g;

最长公共子序列

理解

从减而治之和递归的角度来理解，考虑长度为n的字符串A，长度为m的字符串B，对LCS(n, m)，考虑三种情况：

• 若 $n=0或m=0$，则返回0
• 若 $A[n-1]=B[m-1]$，则返回 $LCS(n-1,m-1)+1$
• 若不相等，则返回 $max(LCS(n-1, m), LCS(n, m-1))$

但是这种方法复杂度极高，甚至是指数级

动态规划版本（感觉像是知道答案写过程一样）

实际上查找的过程可以记录在一张表上：

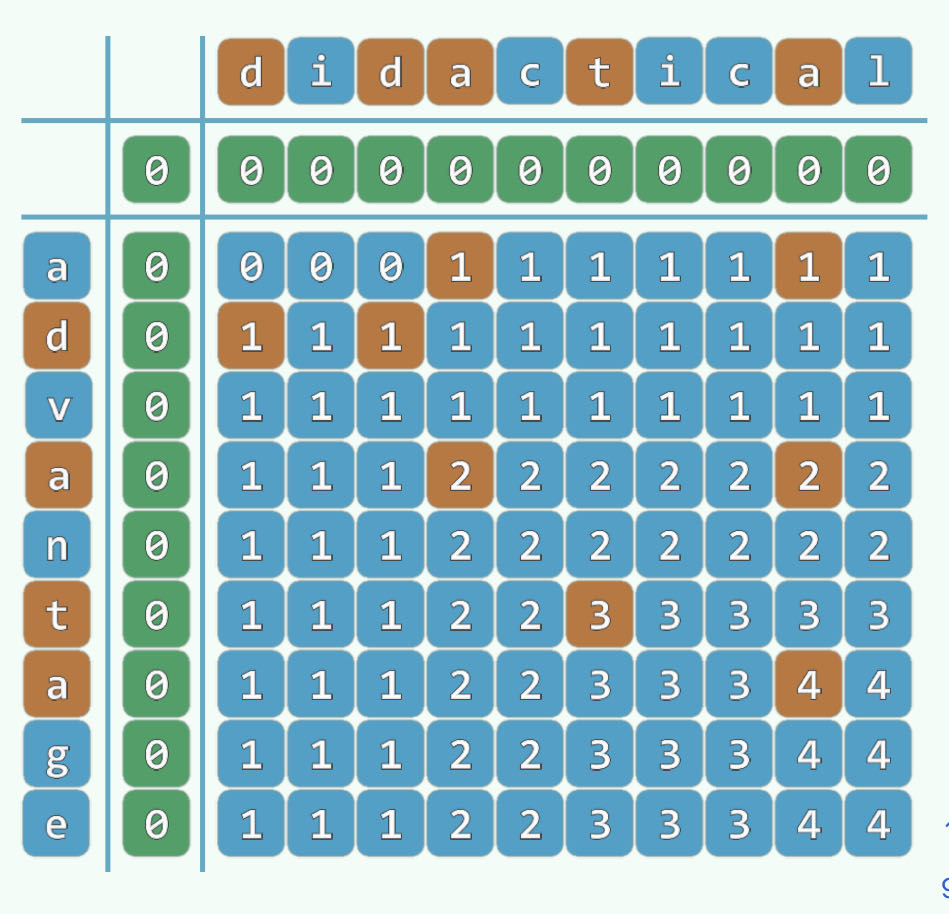
再从递归的角度理解，如果 $A[n-1]=B[m-1]$， $table(n,m)=table(n-1,m-1)+1$，如果不相等，则 $table(n,m)=max(table(n-1,m),table(n,m-1))$

按照这样的规则，我们可以用迭代的方法填写这张表，最终结果即为所求：

这里保证 $m≤n$，一是为了降低空间复杂度，二是降低时间复杂度（这是工程上的问题）